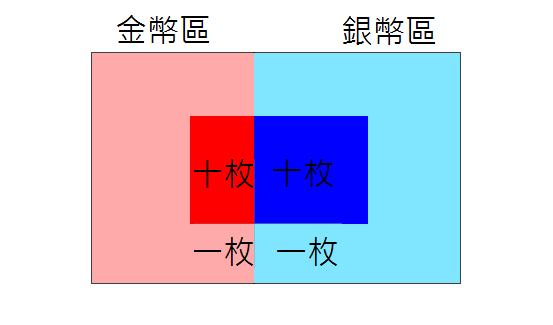
如所示,冒險樂園的一塊標靶上有四個區域,且標靶上任何位置都有同等機會被射中。如果遊戲者射中標靶便勝出:
那麼,遊戲勝出者贏得金幣的概率便是所有紅色區域與標靶面積之比。
現在,已知某甲在一次遊戲後獲得硬幣十枚,請問某甲贏得金幣的概率該如何求得?
由某甲一次贏得硬幣十枚的訊息,我們無需考慮標靶上的淺色區域,則他贏得金幣的概率是正紅色區域與中央正色區域的面積比。
這類問題引伸出條件概率的概念。
在樣本空間\(\;S\;\)中,我們對某事件\(\;A\;\)感興趣。
如果另一事件\(\;B\;\)發生,那麼
在這條件下\(\;A\;\)發生的概率就叫條件概率\(\;P(A丨B)\)。
當樣本空間只有有限個結果且每個結果發生的機會均等時,
\[{P(A丨B)}\color{black}{=\frac{\mbox{同時符合事件}\;A\;\mbox{和}\;B\;\mbox{的結果}}{\mbox{符合事件}\;B\;\mbox{的結果}}}{=\frac{|A\cap B|}{|B|}}\color{black}{。}\]
一般而言,條件概率\(\;P(A丨B)\;\)可由事件\(\;A\cap B\;\)的概率經事件\(\;B\;\)的概率調整所得\[{P(A丨B)=\frac{P(A\cap B)}{P(B)}}\color{black}{。}\]
故此,必須有\(\;P(B)\neq 0\;\)才能討論條件概率\(\;P(A丨B)\;\)。
顯然,條件概率是介乎\(\;0\;\)到\(\;1\;\)的量度。當\(\;A\;\)和\(\;B\;\)為互斥事件時,\(P(A|B)=0\);當\(\;B\;\)為\(\;A\;\)的子集時,\(P(A|B)=1\)。
另一方面,我們也可以利用條件概率求交集的概率\[{P(A\cap B)=P(A|B)\times P(B)}\color{black}{。}\]

這就是條件概率的乘法法則了。
典型的問題中的標靶其實就是個溫氏圖。以下互動素材演示兩個集合\(\;A\;\)和\(\;B\;\)如何分割樣本空間\(\;S\;\)並衍生不同的條件概率的公式。我們假設\(\;P(B),P(\overline{B}),P(A)\;\)和\(\;P(\overline{A})\;\)皆非零,\(\;S\;\)中的結果是有限的且每個結果發生的機會均等。