在上一節,有關雙眼皮學生例子的第三問中,同學可能已見到如何利用條件概率中復原事件本身的概率。
其實我們可以把它歸納為一個簡單而有著廣泛應用的公式:
設\(\;A\;\)和\(\;B\;\)為樣本空間\(\;S\;\)中的兩個事件,當中\(\;P(B)\;\)和\(\;P(\overline{B})\;\)皆非零,則
\[{P(A)=P(A|B)\times P(B)+P(A|\overline{B})\times P(\overline{B})}\color{black}{。}\]
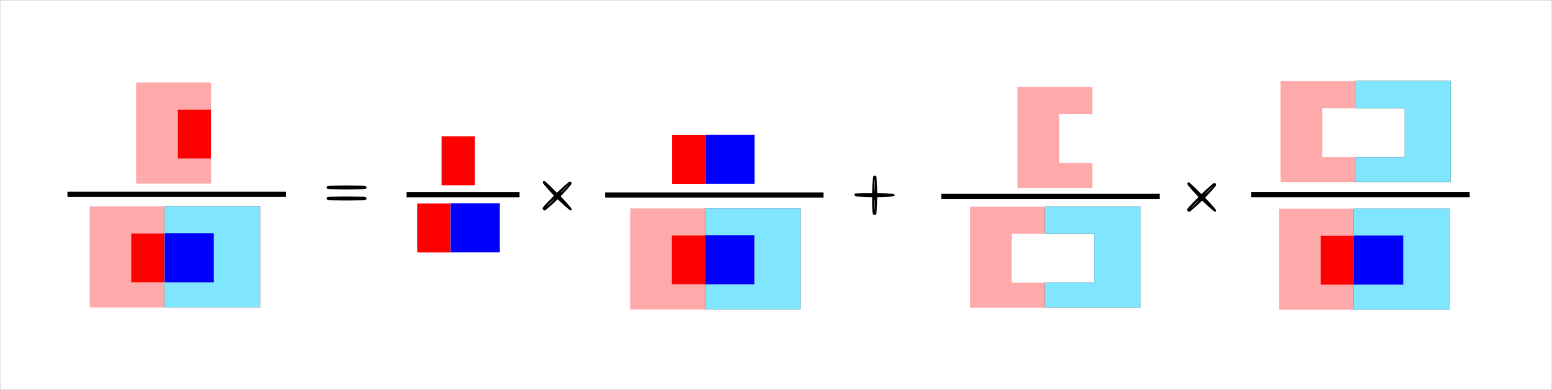
我們稱它為全概率公式
公式有助我們分拆樣本空間為兩個部分來解析事件的概率。
紫鯤有兩個心儀的女生秋蘭和冬梅。他盤算著追求秋蘭成功的概率有\(\;0.3\),追求冬梅成功的概率有\(\;0.1\)。
他現在隨手抓一把小石子,並點算結果以決定向其中一位展開追求:如果石子數目是單數,他就追求秋蘭;如果數目為雙數,他就追求冬梅。請問紫鯤最後追求成功的概率是多少?
\[\begin{align*} &P(\mbox{紫鯤追求成功})\\ =&P(\mbox{追求成功}|\mbox{追求秋蘭})\times P(\mbox{追求秋蘭}) \\ &+ P(\mbox{追求成功}|\mbox{追求冬梅})\times P(\mbox{追求冬梅})\\ =&P(\mbox{追求成功}|\mbox{追求秋蘭})\times P(\mbox{石子數目是單數}) \\ &+ P(\mbox{追求成功}|\mbox{追求冬梅})\times P(\mbox{石子數目是雙數})\\ =&0.3\times 0.5+0.1\times 0.5\\ =&0.2。 \end{align*}\]
更廣義來說,考慮\(\;\displaystyle{n}\;\)個兩兩互斥的事件\(\;B_1,B_2,\dots,B_n\),當中\(\;P(B_1),P(B_2),\dots,P(B_n)\;\)皆非零。如果\(\;B_1\cup B_2\cup \dots\cup B_n=S\),則樣本空間\(\;S\;\)中任一事件\(\;A\;\)的概率可以這樣求得:
\begin{align*} {P(A)=} &P(A|B_1)\times P(B_1)+\\ &{P(A|B_2)\times P(B_2)+\dots+P(A|B_n)\times P(B_n)}\color{black}{。} \end{align*}
因為\[\;B_1\cup B_2\cup \dots\cup B_n=S,\]所以\[\;A=(A\cap B_1)\cup(A\cap B_2)\cup \dots \cup(A\cap B_n);\]
又因為\(\;B_1,B_2,\dots,B_n\;\)兩兩互斥,所以\(\;A\cap B_1,A\cap B_2,\dots,A\cap B_n\;\)也必兩兩互斥。則
\(\begin{align*} &P(A)\\ =&P(A\cap B_1)+P(A\cap B_2)+\dots+P(A\cap B_n)\\ =&P(A|B_1)\times P(B_1)+P(A|B_2)\times P(B_2)+\\ & \dots+P(A|B_n)\times P(B_n)。 \end{align*}\)
紫鵬面前有三個書包:第一個裝有一本數學書和一本物理書;第二個書包比第一個多裝一本化學書;第三個書包又比第二個多裝一本生物書。
他決定隨意拿起一個書包再從中隨意讀一本書,請問紫鵬讀到數學書的概率是多少?

假設事件\(\;A\;\)為紫鵬讀到數學書,事件\(\;B_1\;\)為拿起第一個書包,事件\(\;B_2\;\)為拿起第二個書包,事件\(\;B_3\;\)為拿起第三個書包。則,
\[\begin{align*} &P(A)\\ =&P(A|B_1)\times P(B_1) + P(A|B_2)\times P(B_2) + P(A|B_3)\times P(B_3) \\ =&\frac{1}{2}\times \frac{1}{3} + \frac{1}{3}\times \frac{1}{3} + \frac{1}{4}\times \frac{1}{3} \\ =&\frac{13}{36}。 \end{align*}\]