對於指數函數 \(\displaystyle{f\left( x \right)={{a}^{x}} }\) (\(\displaystyle{ a \gt 0 }\) 且 \(\displaystyle{ a \ne 1 }\)),自變量 \(\displaystyle{ x }\) 可以是任何實數,因此指數函數的定義域是實數的整體,即所有實數。
根據數學實驗可知,指數函數 \(\displaystyle{f\left( x \right)={{a}^{x}} }\) 的圖像與 \(\displaystyle{ x }\) 軸永不相交,且永遠在 \(\displaystyle{ x }\) 軸的上方,\(\displaystyle{ x }\) 軸是指數函數 \(\displaystyle{f\left( x \right)={{a}^{x}}}\) 的水平漸近線,所以指數函數 \(\displaystyle{f\left( x \right)={{a}^{x}} }\) 的值域為所有大於零的實數。
| \(\displaystyle{ a }\) 的範圍 | \(\displaystyle{ a \gt 1 }\) | \(\displaystyle{ 0 \lt a \lt 1 }\) |
|---|---|---|
| 指數函數 \(\displaystyle{y={{a}^{x}} }\) 的圖像 | 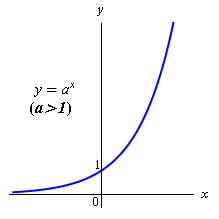 |
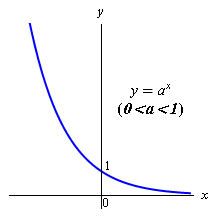 |
| 共同的特性 | 函數的定義域是所有實數,值域是所有大於零的實數。 | |
| 圖像位於 \(\displaystyle{ x }\) 軸上方,與 \(\displaystyle{ x }\) 軸永不相交。 | ||
| 圖像的 \(\displaystyle{ y }\) 軸截距為 \(\displaystyle{1 }\),即圖像與 \(\displaystyle{ y }\) 軸相交於點 \(\displaystyle{\left( 0,1 \right) }\)。 | ||
| 圖像必過點 \(\displaystyle{\left( -1,\frac{1}{a} \right) }\)、\(\displaystyle{\left( 0,1 \right) }\)、\(\displaystyle{\left( 1,a \right) }\)。 | ||
| 圖像沒有極大值點和極小值點,沒有對稱軸,沒有週期性。 | ||
| 圖像有水平漸近線:\(\displaystyle{ x }\) 軸 | ||
| 不同的特性 | 當 \(\displaystyle{ x }\) 從 \(\displaystyle{ 0 }\) 開始不斷減小,函數圖像愈接近於負 \(\displaystyle{ x }\) 軸,即 \(\displaystyle{ y }\) 值會愈來愈接近 \(\displaystyle{ 0 }\),但永遠不會等於 \(\displaystyle{ 0 }\)。 | 當 \(\displaystyle{ x }\) 從 \(\displaystyle{ 0 }\) 開始不斷增大,函數圖像愈接近於正 \(\displaystyle{ x }\) 軸,即 \(\displaystyle{ y }\) 值會愈來愈接近 \(\displaystyle{ 0 }\),但永遠不會等於 \(\displaystyle{ 0 }\)。 |
| 函數圖像從左至右向上傾斜,即當 \(\displaystyle{ x }\) 增加時,函數的值 \(\displaystyle{ y }\) 也增加,該函數是一個遞增的函數。 | 函數圖像從左至右向下傾斜,即當 \(\displaystyle{ x }\) 增加時,函數的值 \(\displaystyle{ y }\) 減少,該函數是一個遞減的函數。 | |
| 當 \(\displaystyle{ x }\) 增加時,函數的值 \(\displaystyle{y }\) 增加的速度愈來愈快,即 \(\displaystyle{ y }\) 的遞增率逐漸增加。 | 當 \(\displaystyle{ x }\) 增加時,函數的值 \(\displaystyle{ y }\) 減少的速度愈來愈慢,即 \(\displaystyle{ y }\) 的遞減率逐漸減少。 | |
當 \(\displaystyle{ a }\) 值愈大時,圖像愈陡峭。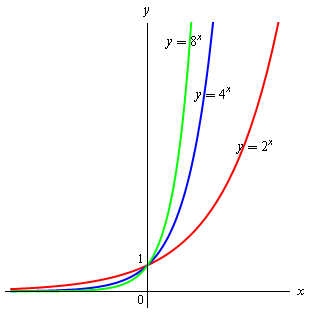 |
當 \(\displaystyle{ a }\) 值愈大時,圖像愈平坦。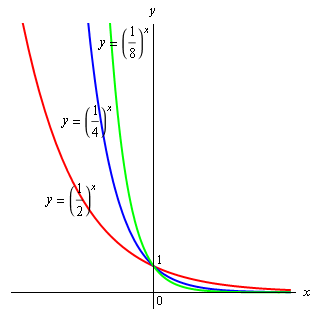 |
|
如圖所示,四個指數函數的圖像,比較各底的大小,其中 \(\displaystyle{ a }\), \(\displaystyle{ b }\), \(\displaystyle{ c }\), \(\displaystyle{ d }\) 均大於 \(\displaystyle{ 0 }\),且不等於 \(\displaystyle{ 1 }\),以下何者是正確的?
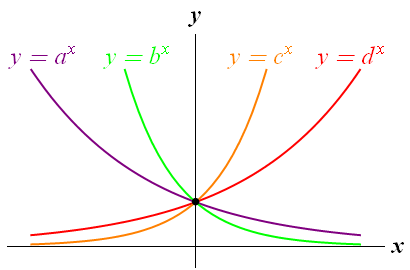
解:選擇 (C)。
方法 1:由指數函數的圖像性質可知:
底大於 \(\displaystyle{ 1 }\) 時,函數是一條遞增曲線,且底愈大,圖像愈陡俏,所以 \(\displaystyle{ c \gt d \gt 1 }\);
底大於 \(\displaystyle{ 0 }\) 小於 \(\displaystyle{ 1 }\) 時,函數是一條遞減曲線,且底愈大,圖像愈平坦,所以 \(\displaystyle{ 0 \lt b \lt a \lt 1 }\)。
方法 2:指數函數 \(\displaystyle{y={{p}^{x}} }\) 與直線 \(\displaystyle{ x = 1 }\) 相交於點 \(\displaystyle{\left( 1,p \right) }\),所以在 \(\displaystyle{ y }\) 軸右側,圖像從下到上相應的底數由小變大,\(\displaystyle{ b \lt a \lt d \lt c }\)。
方法 3:指數函數 \(\displaystyle{y={{p}^{x}} }\) 與直線 \(\displaystyle{ x = -1 }\) 相交於點 \(\displaystyle{\left( -1,\frac{1}{p} \right) }\),所以在 \(\displaystyle{ y }\) 軸左側,圖像從下到上相應的底數由大變小,\(\displaystyle{ c \gt d \gt a \gt b }\)。
指數函數的底數與圖像間的關係可總結為: 在 \(\displaystyle{ y }\) 軸右側 「底大圖高」; 在 \(\displaystyle{ y }\) 軸左側 「底大圖低」。