考慮一個以一般式表示的二次方程 \(ax^2 + bx + c = 0\),其中 \(a \ne 0 \)。
二次公式
\[x = \displaystyle{\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}}\]
從下面 \(3\) 個例子,我們可以看到,\(a\)、\(b\) 及 \(c\) 的不同的值與 \(3\) 個變量的不同值,可導致 \(3\) 種不同的情況:
考慮二次方程 \(x^2 - x - 2 = 0\)。
則 \(a = 1\),\(b = -1\), \(c = -2\)
利用二次公式,
| \(x\) | \(= \displaystyle{\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}}\) |
| \(= \displaystyle{\frac{-(-1) \pm \sqrt{(-1)^2 - 4(1)(-2)}}{2(1)}}\) | |
| \(= \displaystyle{\frac{1 \pm 3}{2}}\) | |
| \(= -1 \, 或 \, 2\) |
\(\therefore\ \, \, 二次方程 \, x^2 - x - 2 = 0\) 的根是\( -1 \, 或 \, 2\) 兩個相異實根。
考慮二次方程 \(4x^2 + 12 x + 9 = 0\)。
則 \(a = 4\),\(b = 12\), \(c = 9\)
利用二次公式,
| \(x\) | \(= \displaystyle{\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}}\) |
| \(= \displaystyle{\frac{-(12) \pm \sqrt{(12)^2 - 4(4)(9)}}{2(4)}}\) | |
| \(= \displaystyle{-\frac{3}{2}}\) |
\(\therefore\ \, \, 二次方程 \, 4x^2 + 12 x + 9 = 0\) 的根是 \(= \displaystyle{-\frac{3}{2}}\) 一個二重實根。
考慮二次方程 \(-x^2 + 2 x - 4 = 0\)。
為了方便計算,我們可將 \(x^2\) 的係數變為正值。因此,
則 \(a = 1\),\(b = -2\), \(c = 4\)
利用二次公式,
\(\begin{align*} x &= \displaystyle{\frac{-(-2) \pm \sqrt{(-2)^2 - 4(1)(4)}}{2(1)}} \\ &= 1 \pm \sqrt{-3}\end{align*}\)
因 \( \sqrt{-3}\) 不是實數,
\(\therefore\;\) 二次方程 \(\, -x^2 + 2 x - 4 = 0\) 沒有實根。
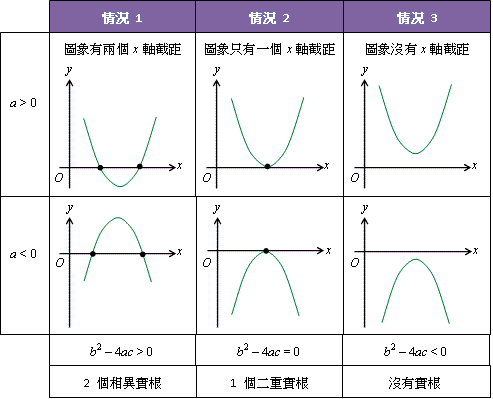
我們於上課已討論過以圖象法解以上三個二次方程。如欲重温詳情,請按此。
考慮一個以一般式表示的二次方程 \(ax^2 + bx + c = 0\),其中 \(a \ne 0 \)。