[興倫智能課堂] 二次方程的求解

數學實驗 —— 讀取二次函數的圖象與 \(x\) 軸的相交點數目

請打開右面的模擬模型，並移動數值滑桿輸入 \(a\)、 \(b\) 與 \(c\) 的數值。請留意輸入不同的數值可導致二次函數 \(y = ax^2 + bx + c\) 圖象出現的變化。

您可以設置以下 \(a\)、 \(b\) 與 \(c\) 的數值進行比較，並填上函數 \(y = ax^2 + bx + c\) 的圖象與 \(x\) 軸相交點的數目：

二次函數	\(a\)	\(b\)	\(c\)	圖象與 \(x\) 軸相交點的數目
函數 \(1\)	\(1\)	\(-1\)	\(-2\)	0 1 2
函數 \(2\)	\(4\)	\(12\)	\(9\)	0 1 2
函數 \(3\)	\(1\)	\(2\)	\(3\)	0 1 2
函數 \(4\)	\(-1\)	\(2\)	\(-4\)	0 1 2
函數 \(5\)	\(-2\)	\(-8\)	\(-8\)	0 1 2
函數 \(6\)	\(-3\)	\(2\)	\(8\)	0 1 2

我們可以觀察到二次函數 \(y = ax^2 + bx + c\) 的圖象與 \(x\) 軸的相交點的數目為 \(1\) 或 \(2\) 或完全不相交。相交點的數目完全取決於二次函數的圖象。

圖象法解二次方程

考慮二次函數 \(y = x^2 - x - 2\)。

圖象與 \(x\) 軸的相交於 \(2\) 點。
第一個相交點的坐標是 (\(-1, 0\))，即這點的 \(x\) 坐標 \(-1\) 為曲線的 \(x\) 軸截距。
第二個相交點的坐標是 (\(2, 0\))，即這點的 \(x\) 坐標 \(2\) 為曲線的 \(x\) 軸截距。
在 \(y = x^2 - x - 2\) 的圖象中，\(x\) 軸截距是 \(-1\) 和 \(2\) 是當 \(y = 0\)，即 \(x^2 - x - 2 = 0\) 時的 \(x\) 值。
因此，\(-1\) 和 \(2\) 是二次方程 \(x^2 - x - 2 = 0\) 的根。

根據以上的說法，從右面的模擬模型所顯示的二次函數的圖象，可得：

二次方程	根的數目	根	根
\(x^2 - x - 2 = 0\)	\(2\)	\(-1\)	\(2\)
\(4x^2 + 12x + 9 = 0\)	\(1\)	\(-\displaystyle{\frac{3}{2}}\)	- - -
\(x^2 + 2x + 3 = 0\)	\(0\)	- - -	- - -
\(-x^2 + 2x - 4 = 0\)	\(0\)	- - -	- - -
\(-2x^2 - 8x - 8 = 0\)	\(1\)	\(-2\)	- - -
\(-3x^2 + 2x - 8 = 0\)	\(2\)	\(-\displaystyle{\frac{4}{3}}\)	\(2\)

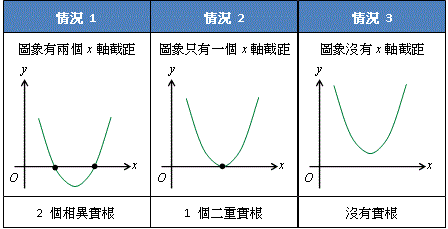
根據上面的模擬模型所得，二次函數 \(y = x^2 - x - 2\) 的圖象中的 \(x\) 軸截距的數目有以下有三種不同的情況：