考慮二次函數 \(y = x^2 - x - 2\)。
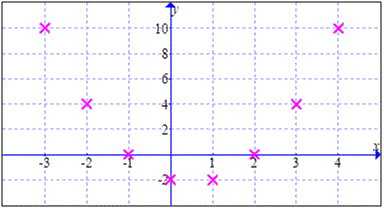
下表顯示在不同的 \(x\) 值下的相應 \(y\) 值。
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
|---|---|---|---|---|---|---|---|---|
| \(x^2\) | \(9\) | \(4\) | \(-1\) | \(0\) | \(1\) | \(4\) | \(9\) | \(16\) |
| \(-x\) | \(3\) | \(2\) | \(1\) | \(0\) | \(-1\) | \(-2\) | \(-3\) | \(-4\) |
| \(-2\) | \(-2\) | \(-2\) | \(-2\) | \(-2\) | \(-2\) | \(-2\) | \(-2\) | \(-2\) |
| \(y\) | \(10\) | \(4\) | \(0\) | \(-2\) | \(-2\) | \(0\) | \(4\) | \(10\) |
我們可以觀察到以下有關二次函數 \(y = ax^2 + bx + c\) 的圖象。
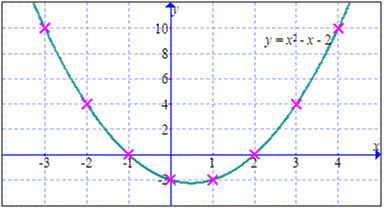
繪畫 \(y = x^2 - x - 2\) 的圖象的步驟:
繪畫直角坐標。
繪製點 \( (x, y) \)。
繪畫 \(y = x^2 - x - 2\) 的圖象。