在樣本空間\(\;\displaystyle{S}\;\)中,事件\(\;\displaystyle{A}\;\)或事件\(\;\displaystyle{B}\;\)發生的概率(不排除兩者同時發生)就是事件\(\;\displaystyle{A\cup B}\;\)發生的概率。
利用互斥事件的加法法則,我們可以推導出一般事件的加法定律。
如互動素材所示,任意事件\(\;\displaystyle{A}\;\)和\(\;\displaystyle{B}\;\)滿足:
\[{P(A\cup B) = P(A)+P(B)-P(A\cap B)}\;\color{black}{;}\]
以上等式中,事件\(\;A\cap B\;\)是指事件\(\;\displaystyle{A}\;\)和事件\(\;\displaystyle{B}\;\)同時發生。
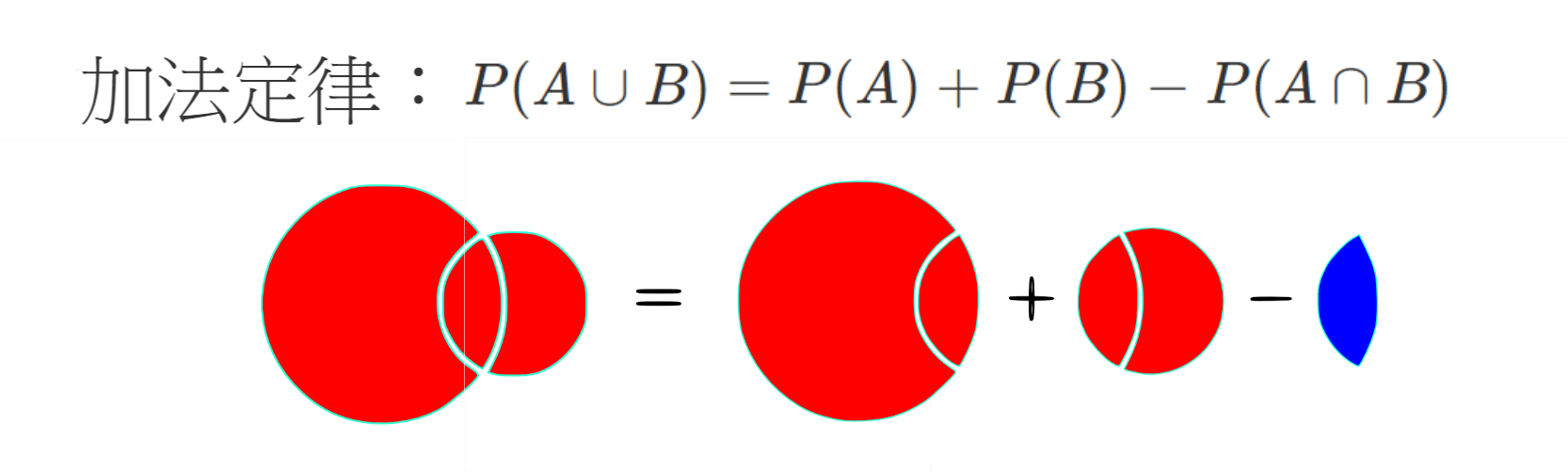 |
 |
 |
 |
 |
 |
按下一步看推導過程。
\[\begin{align*} &\phantom{P(\color{red}{A \cup B})}\\ \phantom{=}&\phantom{P(A)+P(\overline{A} \cap B)}\\ \phantom{=}&\phantom{P(A\cap\overline{B})+P(A\cap B)+P(\overline{A} \cap B)}\\ \phantom{=}&\phantom{[P(A\cap\overline{B})+P(A\cap B)]+[P(A\cap B)+P(\overline{A} \cap B)]-P(A\cap B)}\\ \phantom{=}&\phantom{P(A)+P(B)-P(A\cap B)} \end{align*}\]\[\begin{align*} &P(\color{red}{A \cup B})\\ \phantom{=}&\phantom{P(A)+P(\overline{A} \cap B)}\\ \phantom{=}&\phantom{P(A\cap\overline{B})+P(A\cap B)+P(\overline{A} \cap B)}\\ \phantom{=}&\phantom{[P(A\cap\overline{B})+P(A\cap B)]+[P(A\cap B)+P(\overline{A} \cap B)]-P(A\cap B)}\\ \phantom{=}&\phantom{P(A)+P(B)-P(A\cap B)} \end{align*}\]
\[\begin{align*} &P(A \cup B)\\ =&P(\color{red}{A})+P(\color{red}{\overline{A} \cap B})\\ \phantom{=}&\phantom{P(A\cap\overline{B})+P(A\cap B)+P(\overline{A} \cap B)}\\ \phantom{=}&\phantom{[P(A\cap\overline{B})+P(A\cap B)]+[P(A\cap B)+P(\overline{A} \cap B)]-P(A\cap B)}\\ \phantom{=}&\phantom{P(A)+P(B)-P(A\cap B)} \end{align*}\]
提示:觀察到\(\;A\cup( \overline{A} \cap B)=A\cup B\;\)和\(\;A\cap( \overline{A} \cap B)=\emptyset \);根據互斥事件的加法法則,\(P(A\cup B)=P(A)+P( \overline{A} \cap B)\)。
\[\begin{align*} &P(A \cup B)\\ =&P(A)+P(\overline{A} \cap B)\\ =&P(\color{red}{A\cap\overline{B}})+P(\color{red}{A\cap B})+P(\color{red}{\overline{A} \cap B})\\ \phantom{=}&\phantom{[P(A\cap\overline{B})+P(A\cap B)]+[P(A\cap B)+P(\overline{A} \cap B)]-P(A\cap B)}\\ \phantom{=}&\phantom{P(A)+P(B)-P(A\cap B)} \end{align*}\]
提示:觀察到\(\;(A\cap \overline{B}) \cup (A\cap B)=A\;\)和\(\;(A\cap \overline{B}) \cap (A\cap B)=\emptyset \);根據互斥事件的加法法則,\(P(A)=P(A \cap \overline{B})+P(A\cap B)\)。
\[\begin{align*} &P(A \cup B)\\ =&P(A)+P(\overline{A} \cap B)\\ =&P(A\cap\overline{B})+P(A\cap B)+P(\overline{A} \cap B)\\ =&[P(\color{red}{A\cap\overline{B}})+P(\color{red}{A\cap B})]+[P(\color{red}{A\cap B})+P(\color{red}{\overline{A} \cap B})]-P(\color{blue}{A\cap B})\\ \phantom{=}&\phantom{P(A)+P(B)-P(A\cap B)} \end{align*}\]
\[\begin{align*} &P(A \cup B)\\ =&P(A)+P(\overline{A} \cap B)\\ =&P(A\cap\overline{B})+P(A\cap B)+P(\overline{A} \cap B)\\ =&[P(A\cap\overline{B})+P(A\cap B)]+[P(A\cap B)+P(\overline{A} \cap B)]-P(A\cap B)\\ =&P(\color{red}{A})+P(\color{red}{B})-P(\color{blue}{A\cap B}) \end{align*}\]
提示:根據互斥事件的加法法則,\(P(A)=P(A\cap B)+ P(A \cap \overline{B})\),\(P(B)=P(A\cap B)+ P(\overline{A} \cap B)\)。
這定律有著廣泛的實際應用:

擲一枚有六面各刻上\(\;1\;\)至\(\;6\;\)的骰子,擲到\(\;2\;\)的倍數或\(\;3\;\)的倍數的概率是: \[\begin{align*} &P(\mbox{擲到}\;2\;\mbox{的倍數或}\;3\;\mbox{的倍數的概率})\\ =&P(\mbox{擲到}\;2\;\mbox{的倍數})+P(\mbox{擲到}\;3\;\mbox{的倍數})-P(\mbox{擲到}\;6\;\mbox{的倍數})\\ =&\frac{1}{2}+\frac{1}{3}-\frac{1}{6}\\ =&\frac{2}{3}\;。 \end{align*}\]
在一套共\(\;52\;\)張啤牌中抽一張,抽中紅心或抽中牌面\(\;Q\;\)的概率是: \[\begin{align*} &P(\mbox{抽中紅心或}\;Q)\\ =&P(\mbox{抽中紅心})+P(\mbox{抽中}\;Q)-P(\mbox{抽中}\;\color{red}{\heartsuit \;Q})\\ =&\frac{13}{52}+\frac{4}{52}-\frac{1}{52}\\ =&\frac{4}{13}\;。 \end{align*}\]

| \(P(A\cup B)\) | \(P(A)+ P(B)\) |
題解:
給定任何事件\(\;A\;\)和\(\;B\),\(P(A\cap B)\geq 0\)。
根據加法定律 \[\begin{align*} &P(A\cup B)\\ =& P(A)+P(B)-P(A\cap B)\\ \leq& P(A)+P(B)。 \end{align*}\]