在物理學上,聲音強度的單位是 \(\displaystyle{ {W}/{ { {m}^{2}}}\; }\) ( 瓦特/平方米 ),如正常人的耳朵可以聽到的聲音強度一般是由 \(\displaystyle{ { {10}^{-12}} }\) 到 \(\displaystyle{ 1 }\) \(\displaystyle{ {W}/{ { {m}^{2}}}\; }\),範圍十分廣,但用這種單位來表示聲音的大小非常不方便,使用對數標度會更好。因此,我們通常用另一種單位來表示聲音的大小:音量。
音量的單位叫分貝 (decibel),用符號 \(\rm{dB}\) 表示。
一個聲音強度為 \(\displaystyle{ I }\) 的聲音, 其音量 \(\displaystyle{ D }\) 定義為: \[ D=10\log \frac{I}{ { {I}_{0}}} \] 其中,\(\displaystyle{ { {I}_{0}}={ {10}^{-12}} }\) \(\displaystyle{ {W}/{ { {m}^{2}}}\; }\) 表示一般人能聽見的最低聲音強度。 \(\displaystyle{ { {I}_{0}} }\) 對應的音量是 \(\displaystyle{0 }\) \(\rm{dB}\), 其他聲音的音量可以視為與 \(\displaystyle{ { {I}_{0}} }\) 作比較後得到的。
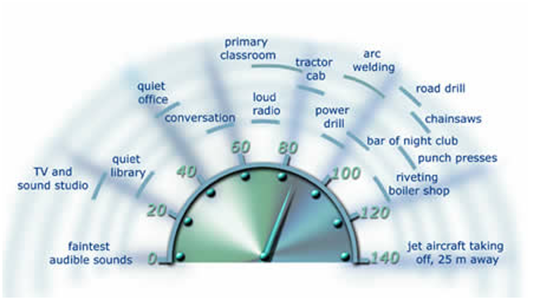
例 \(1\):香港尖沙咀彌敦道某路段的平均聲音強度為 \(\displaystyle{4\times { {10}^{-3}} }\) \(\displaystyle{ {W}/{ { {m}^{2}}}\; }\), 求該路段的平均音量 ( 以 \(\rm{dB}\) 為單位 )。
( 答案準確至最接近的整數 )
解:該路段的平均音量
\(\begin{align*} D &= 10\log \frac{I}{ { {I}_{0}}} \\
&= 10\log \frac{4\times { {10}^{-3}}}{ { {10}^{-12}}} \\
&= 10\log \left( 4\times { {10}^{9}} \right) \\
& \approx 96 \end{align*}\)
所以該路段的平均音量為 \(96\) \(\rm{dB}\)。
例 \(2\):某學生的物理老師的音量比化學老師的音量高 \(\displaystyle{ 4 }\) \(\rm{dB}\),求該學生的物理老師和化學老師的聲音強度的比。
(答案以 \(\displaystyle{ n:1 }\) 的形式出現,其中 \(\displaystyle{ n }\) 準確至一位小數)
解: 設該學生的物理老師和化學老師的聲音強度分別為 \(\displaystyle{ { {I}_{p}} }\) 和 \(\displaystyle{ { {I}_{c}} }\)
\(\displaystyle{10\log \frac{ { {I}_{p}}}{ { {I}_{0}}}-10\log \frac{ { {I}_{c}}}{ { {I}_{0}}}=4 }\)
\(\displaystyle{\therefore \log \left( \frac{ { {I}_{p}}}{ { {I}_{0}}}\div \frac{ { {I}_{c}}}{ { {I}_{0}}} \right)=\frac{4}{10} }\)
\(\displaystyle{\therefore \frac{ { {I}_{p}}}{ { {I}_{c}}}={ {10}^{0.4}}\approx 2.5 }\)
所以該學生的物理老師和化學老師的聲音強度的比是 \(\displaystyle{2.5 : 1 }\)。
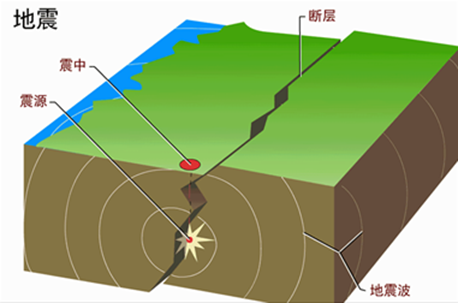
地震的震级是根據地震儀器探測和記錄的地震波振幅來測定的,通常以黎克特製震級 (Richter magnitude scale) 表示,將地震分級。該制是由美國地震學家古騰堡 (Beno Cutenberg,\(1889-1960\)) 和黎克特 (Charles F. Richter,\(1900-1985\)) 於 \(1935\) 年共同提出。

黎克特製地震震級 (\(\displaystyle{ M }\)) 的公式運用了對數函數: \[M=\log \frac{A}{ { {A}_{0}}} \]
其中,\(\displaystyle{ A }\) 是指該地震在距震央 \(\displaystyle{ 100 }\) 公里處接收到的地震波之最大震幅,單位是 \(\displaystyle{ μm }\) ; \(\displaystyle{ { {A}_{0}} }\) 是距震央 \(\displaystyle{100 }\) 公里處接收到的 \(\displaystyle{ 0 }\) 級地震的地震波之最大震幅,單位是 \(\displaystyle{ μm }\)。
黎克特製地震震級 (\(\displaystyle{ M }\)) 的大小與震源中心釋放的能量 ( 熱能和動能 ) 大小有關,震源釋放的能量越大,震級就越大。
黎克特製地震震級 (\(\displaystyle{ M }\)) 的公式也可用震源所釋放的能量來表示: \[M=\frac{2}{3}\log \frac{E}{ { {E}_{0}}} \]
其中 \(\displaystyle{ E }\) 表示該地震所釋放的能量,單位為焦耳 ( \(\displaystyle{ J }\) );\(\displaystyle{ { {E}_{0}} }\) 是小型參考地震所釋放的能量, 值為 \(\displaystyle{ { {10}^{4.8}} }\) 焦耳 ( \(\displaystyle{ J }\) )。
思考:如果黎克特製地震震級 (\(\displaystyle{ M }\)) 每增加一級,那麼該地震在距震央 \(\displaystyle{ 100 }\) 公里處接收到的地震波之最大震幅增加至多少倍?其所釋放的熱能量又增大至多少倍呢?
解:假設第 \(\displaystyle{ n }\) 級地震在距震央 \(\displaystyle{ 100 }\) 公里處接收到的地震波之最大震幅表示為 \(\displaystyle{ { {A}_{n}} }\),
第 \(\displaystyle{ n }\) 級地震所釋放的能量表示為 \(\displaystyle{ { {E}_{n}} }\),那麼:
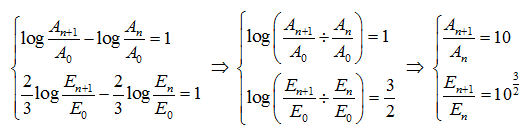
所以,黎克特製地震震級 (\(\displaystyle{ M }\)) 每增加一級,表示地震在距震央 \(\displaystyle{ 100 }\) 公里處接收到的地震波之最大震幅增至 \(\displaystyle{ 10 }\) 倍,其所釋放的熱能量增至 \(\displaystyle{10\sqrt{10} }\) 倍。假定第一級地震所釋放的能量為 \(\displaystyle{ K }\),那麼第二級地震所釋放的能量應為 \(\displaystyle{10\sqrt{10} }\) \(\displaystyle{ K }\) \(\displaystyle{ \approx 31.62 }\) \(\displaystyle{ K }\),第三級為 \(\displaystyle{ 1000 }\) \(\displaystyle{ K }\),第七級為 \(\displaystyle{ 10 }\) 億 \(\displaystyle{ K }\),第九級就是 \(\displaystyle{ 1 }\) 萬億 \(\displaystyle{ K }\)。
由此可知,\(1976\) 年 \(\displaystyle{ 7.8 }\) 級的唐山大地震,\(2008\) 年的 \(\displaystyle{ 8.0 }\) 級汶川地震,以及歷史紀錄中最強烈的 \(1960\) 年的 \(\displaystyle{ 8.9 }\) 級智利大地震造成的危害有多大。
例題:中華人民共和國成立以來,其中破壞性最强、波及範圍最廣、總傷亡人數最多的幾次地震包括 \(1976\) 年的唐山大地震和 \(2008\) 年的汶川地震。 根據黎克特製地震震級的標準,唐山大地震是 \(\displaystyle{ 7.8 }\) 級,汶川地震是 \(\displaystyle{ 8.0 }\) 級。
求汶川地震所釋放的能量是唐山大地震的多少倍? ( 答案準確至最接近的整數 )
設汶川地震所釋放的能量是唐山大地震的 \(\displaystyle{ x }\) 倍,則 \(\displaystyle{\frac{2}{3}\log \frac{x{ {E}_{1}}}{ { {E}_{0}}}=8 }\)
\(\displaystyle{\because \frac{2}{3}\log \frac{x{ {E}_{1}}}{ { {E}_{0}}}=\frac{2}{3}\log x+\frac{2}{3}\log \frac{ { {E}_{1}}}{ { {E}_{0}}} }\)
\(\displaystyle{\therefore 8=\frac{2}{3}\log x+7.8 }\)
\(\displaystyle{\therefore \log x=0.3 }\)
\(\displaystyle{\therefore x={ {10}^{0.3}}\approx 2 }\) (準確至最接近的整數)
所以汶川地震所釋放的能量是唐山大地震的 \(\displaystyle{ 2 }\) 倍。