指數函數常用來描述自然界許多有關成長及衰退的模式,它的產生是很自然的,相應的也產生了其反函數——對數函數。
在自然科學及社會科學裡,某些函數 \(\displaystyle{N\left( t \right) }\) 的變化常常遵循以下法則:
\(\displaystyle{N\left( t \right) }\) 在時間 \(\displaystyle{ t }\) 的變化率與在 \(\displaystyle{ t }\) 時的量 \(\displaystyle{N\left( t \right) }\) 成比率。若要把這個法則寫成表達式,需借助之後學到的導數概念,解導數方程後,可得到表達式為:
\(\displaystyle{N\left( t \right)={ {N}_{0}}{ {e}^{kt}} }\),其中 \(\displaystyle{ { {N}_{0}} }\) 為初始值,即 \(\displaystyle{ t=0 }\) 時,\(\displaystyle{N\left( 0 \right)={ {N}_{0}} }\);\(\displaystyle{ k }\) 是比率常數,稱為成長常數。
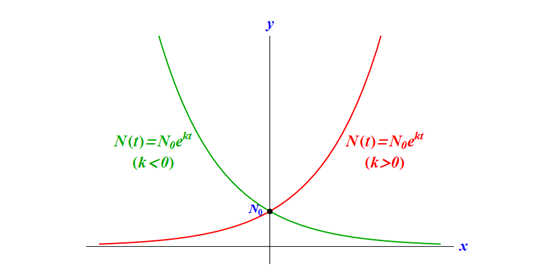
指數增長與指數衰退的模型:\(\displaystyle{N\left( t \right)={ {N}_{0}}{ {e}^{kt}} }\) (自然指數)。
當 \(\displaystyle{ k \gt 0}\) 時,\(\displaystyle{\mathrm{N}\left( \mathrm{t} \right) }\) 為指數增長 (exponential growth)。
當 \(\displaystyle{ k \lt 0 }\) 時,\(\displaystyle{\mathrm{N}\left( \mathrm{t} \right) }\) 為指數衰退 (exponential decay)。
現實生活中的許多現象都符合指數增長/指數衰退的模型,例如:
經濟學:存款的複利問題 (包括連續複利問題)、傳銷、物品折舊和國民生產總值的增長等;
生物學:種群增長 (如人口的增長)、微生物的繁殖和細菌的傳播等;
物理學:放射性物質的衰變、核鏈式反應和熱傳遞等;
計算機學:電腦的處理效率問題和互聯網流量增長等。
種群增長是種群動態的主要表現形式之一。隨著時間的變化,一個種群個體數目會不斷增加。種群增長,包括人口的增長,一般都遵從指數增長模型。例如某地區現時的人口是 \(\displaystyle{ {P}_{0} }\),每年將以 \(\displaystyle{s\% }\) 的速度穩定增長,那麼 \(\displaystyle{ n }\) 年後該地區的人口 \(\displaystyle{P\left( n \right)={ {P}_{0}}{ {\left( 1+s\% \right)}^{n}} }\)。

例 \(1\):某一城市的人口數量 \(\displaystyle{A\left( t \right) }\) 與時間 \(\displaystyle{ t }\) 的關係為 \(\displaystyle{P\left( t \right)=5{ {e}^{0.02t}} }\), \(\displaystyle{P\left( t \right) }\) 以萬為單位,\(\displaystyle{ t }\) 以 \(2012\) 年為起始值,即 \(\displaystyle{ t=0 }\) 表示 \(2012\) 年年初。 根據此指數增長模型回答以下問題:
該城市在 \(2012\) 年年初的人數有多少?
該城市在 \(2020\) 年年初的人數是多少? ( 答案準確至三位小數 )
該城市每年人口增長的速度是多少? ( 答案以百分比的形式表示,準確至兩位小數 )
該城市的人口約在哪一年能達到 \(\displaystyle{ 10 }\) 萬?
解:
(1) 該城市在 \(2012\) 年年初的人數即為 \(\displaystyle{P\left( 0 \right)=5{ {e}^{0.02\times 0}}=5 }\) 萬。
(2) 該城市在 \(2020\) 年年初的人數即為 \(\displaystyle{P\left( 8 \right)=5{ {e}^{0.02\times 8}} }\),約為 \(\displaystyle{ 5.868 }\) 萬。
\(\begin{align*} (3) \ \frac{P\left( t+1 \right)}{P\left( t \right)} &= \frac{5{ {e}^{0.02\left( t+1 \right)}}}{5{ {e}^{0.02t}}} \\ &= { {e}^{0.02}} \\ & \approx 1.0202 \end{align*}\)
所以,該城市人口每年增長 \(\displaystyle{ 2.02\% }\)。
\(\begin{align*} (4) \ P\left( t \right) &= 5{ {e}^{0.02t}} \\ &= 10 \\ t &= \frac{\ln 2}{0.02} \\ & \approx 34.66 \end{align*}\)
所以,該城市大約在 \(\displaystyle{ 34.66 }\) 年後,即 \(2046\) 年下半年的時候,人口將達到 \(\displaystyle{ 10 }\) 萬。
例 \(2\):某一果園的果蠅的成長率和當時的果蠅數成比率,即符合指數增長模型,果蠅數 \(\displaystyle{N\left( t \right) }\) 可以表示為時間 \(\displaystyle{ t }\) 天的函數:\(\displaystyle{N\left( t \right)={ {N}_{0}}{ {e}^{kt}} }\)。 若在開始時有 \(\displaystyle{ 100 }\) 隻果蠅,第 \(\displaystyle{ 5 }\) 天時果蠅數翻倍,試問 \(\displaystyle{ 10 }\) 天後果蠅的總數是多少?

第 \(\displaystyle{ 5 }\) 天果蠅數翻倍,則 \(\displaystyle{N\left( 5 \right)=200 }\)
\(\displaystyle{\therefore N\left( 0 \right)={ {N}_{0}}=100 }\)
\(\displaystyle{\therefore N\left( 5 \right)={ {N}_{0}}{ {e}^{5k}}=200\Rightarrow k=\frac{\ln 2}{5} }\)
\(\displaystyle{ 10 }\) 天後果蠅的總數為:
\(\begin{align*} \ \ \ \ N\left( 10 \right) &= { {N}_{0}}{ {e}^{10k}} \\
&= 100\times { {e}^{2\ln 2}} \\
&= 400 \end{align*}\)
所以,\(\displaystyle{ 10 }\) 天後果蠅的總數是 \(\displaystyle{ 400 }\) 隻。
假設將本金 \(\displaystyle{ { {N}_{0}} }\) 元存入銀行中,銀行的存款利率是 \(\displaystyle{ r }\),每年複利一次,那麼 \(\displaystyle{ t }\) 年後的本利和 ( 本金加利息的和 ) 為 \(\displaystyle{N\left( t \right)={ {N}_{0}}{ {\left( 1+r \right)}^{t}} }\)。這種本金的增長模式與種群的增長模式類似。以下考慮一個連續增長,即連續複利的問題。
銀行的利率通常以年利率為準,但有些銀行可能依顧客的需求而縮短複利的時間,例如每半年複利一次,即每年複利兩次;或是每季複利一次,即每年複利四次;或每月複利一次,即每年複利十二次。

假設將本金 \(\displaystyle{ { {N}_{0}} }\) 元存入銀行,年利率為 \(\displaystyle{ r }\) 且每年複利 \(\displaystyle{ n }\) 次, 即每 \(\displaystyle{\frac{365}{n} }\) 天複利一次,每次複利的利率為 \(\displaystyle{\frac{r}{n} }\), 那麼 \(\displaystyle{ t }\) 年後的本利和為 \(\displaystyle{N\left( t \right)={ {N}_{0}}{ {\left( 1+\frac{r}{n} \right)}^{nt}} }\)。
根據常數 \(\displaystyle{ e }\) 的產生原理,\(\displaystyle{n\to \infty }\) 時,\(\displaystyle{ { {\left( 1+\frac{1}{n} \right)}^{n}}=e }\), 所以當 \(\displaystyle{ n\to \infty }\) 時,\(\displaystyle{N\left( t \right)={ {N}_{0}}{ {\left[ { {\left( 1+\frac{r}{n} \right)}^{\frac{n}{r}}} \right]}^{rt}}={ {N}_{0}}{ {e}^{rt}} }\)。 \(\displaystyle{n\to \infty }\) 理論上是可行的,即在愈來愈短的時間內複利一次,此情況稱為連續複利。
結論1:連續複利問題是一個典型的指數增長實例。將本金 \(\displaystyle{ { {N}_{0}} }\) 元存於年利率為 \(\displaystyle{ r }\) 的銀行裡, 在連續複利的情況下,\(\displaystyle{ t }\) 年後的本利和為 \(\displaystyle{N\left( t \right)={ {N}_{0}}{ {e}^{rt}} }\)。
逆向思考:在年利率為 \(\displaystyle{ r }\) 且每年複利 \(\displaystyle{ n }\) 次的情況下, 假設 \(\displaystyle{ t }\) 年後可以拿回的本利和為 \(\displaystyle{N\left( t \right) }\),那麼 \(\displaystyle{ { {N}_{0}} }\) 即所謂的現值, 因此現值 \(\displaystyle{ { {N}_{0}}=N\left( t \right){ {\left( 1+\frac{r}{n} \right)}^{-nt}} }\); 在年利率為 \(\displaystyle{ r }\) 且連續複利的情況下,現值 \(\displaystyle{ { {N}_{0}}=N\left( t \right){ {e}^{-rt}} }\)。
結論2:假設銀行的年利率為 \(\displaystyle{ r }\),連續複利,那麼 \(\displaystyle{ t }\) 年後 \(\displaystyle{ N }\) 元的現值為 \(\displaystyle{ { {N}_{0}}=N{ {e}^{-rt}} }\)。
例題:華仔預計在 \(\displaystyle{ 3 }\) 年後投資 \(\displaystyle{70 }\) 萬元開一家小餐館,假設銀行的年利率是 \(\displaystyle{ 3\% }\), 以連續複利計算,請問他現在應該存多少錢在銀行,才能實現他的投資計畫? ( 答案準確至三位小數 )
解:由題意對應公式 \(\displaystyle{ { {N}_{0}}=N\left( t \right){ {e}^{-rt}} }\) 知:\(\displaystyle{N=70 }\),\(\displaystyle{r=3\% }\),\(\displaystyle{ t=3 }\)。
則:\(\displaystyle{ { {N}_{0}}=70{ {e}^{-0.03\times 3}}\approx 63.975 }\) 萬元
即華仔現在應該存 \(\displaystyle{ 63.975 }\) 萬元在銀行,\(\displaystyle{ 3 }\) 年後就能實現他的投資計畫。
思考:運用對數函數求年限
假設將本金 \(\displaystyle{ { {N}_{0}} }\) 元存入年利率為 \(\displaystyle{ r }\)、連續複利的銀行中,請問多少年後可以拿回 \(\displaystyle{ N }\) 元本利和?
解:\(\displaystyle{N\left( t \right)={ {N}_{0}}{ {e}^{rt}} }\),則 \(\displaystyle{t=\frac{1}{r}\ln \frac{N\left( t \right)}{ { {N}_{0}}} }\)。
耐用品,例如汽車、手機、相機和家電等的價值在使用一段時間後,其價值會減低,也稱折舊。若一個購入價為 \(\displaystyle{ { {A}_{0}} }\) 元的單反相機,價值每年都減少 \(\displaystyle{ d\% }\),那麼 \(\displaystyle{ n }\) 年後該單反相機的價值為 \(\displaystyle{A\left( n \right)={ {A}_{0}}{ {\left( 1-d\% \right)}^{t}} }\)。折舊物品的價值呈指數性衰退。
例題:某型號汽車現時的購買價是 \(\displaystyle{20 }\) 萬,汽車的價值隨著時間的推移而不斷降低。該汽車在第 \(\displaystyle{ t }\) 年的價值 \(\displaystyle{A\left( t \right)={ {A}_{0}}{ {e}^{-0.25t}} }\) 萬元。問:
該汽車每年折舊多少? ( 答案以百分比的形式表示,準確至兩位小數 )
多少年後,該汽車的價值降到購買價的一半? ( 答案準確至整數個年和整數個月 )
解:
購買價為 \(\displaystyle{ 20 }\) 萬,所以 \(\displaystyle{A\left( 0 \right)={ {A}_{0}}=20}\);
\(\begin{align*} (1) \ \frac{A\left( t+1 \right)}{A\left( t \right)} &= \frac{ { {A}_{0}}{ {e}^{-0.25\left( t+1 \right)}}}{ { {A}_{0}}{ {e}^{-0.25t}}} \\ &= { {e}^{-0.25}} \\ & \approx 0.7788 \end{align*}\)
折舊率約為 \(\displaystyle{\left( 1-0.7788 \right)=0.2212 }\)
所以該汽車每年折舊約為 \(\displaystyle{ 22.12\% }\)。
\(\begin{align*} (2) \ A\left( t \right) &= { {A}_{0}}{ {e}^{-0.25t}} \\ &= \frac{1}{2}{ {A}_{0}} \\ t &= -\frac{1}{0.25}\ln \frac{1}{2} \\ & \approx 2.773 \end{align*}\)
所以該汽車在購買的大約兩年九個月後,該汽車的價值就降到購買價的一半。

放射性元素,例如釙 (\(Po\))、氡 (\(Rn\))、鈁 (\(Fr\))、鐳 (\(Ra\))、錒 (\(Ac\))、釷 (\(Th\))、鏷 (\(Pa\)) 和鈾 (\(U\)) 等,他們會衰變而散發輻射 (如 \(\displaystyle{ \alpha }\) 射線、\(\displaystyle{\beta }\) 射線等 ),質量減少。科學家發現,一個質量為 \(\displaystyle{ { {w}_{0}} }\)\(\displaystyle{ kg }\) 的放射性物質經過 \(\rm{t}\) 年後,其重量衰變為 \(\displaystyle{w\left( t \right)={ {w}_{0}}{ {e}^{-\gamma t}}\left( \gamma \gt 0 \right) }\),其中 \(\displaystyle{ \gamma }\) 是一個關於該放射性物質的屬性的正值常數。放射性物質的衰變是一個典型的指數衰退模型的實例。根據此公式,放射性物質常用來測定年代。
例題:\(A\) 與 \(B\) 兩種放射性物質,他們的衰變情況如下:\(\displaystyle{ t }\) 年後,\(A\) 與 \(B\) ( 以磅為單位 ) 的質量分別為 \(\displaystyle{A(t)=12{ {e}^{-0.009t}} }\),\(\displaystyle{B(t)=3{ {e}^{-0.003t}} }\)。
試問:(1) \(A\) 與 \(B\) 最初的質量比是多少?
(2) \(\displaystyle{ 100 }\) 年後,\(A\) 與 \(B\) 的質量比又是多少? ( 答案以 \(\displaystyle{ n:1 }\) 的形式出現,其中 \(\displaystyle{ n }\) 準確至一位小數 )
解:(1) 最初的時候,即 \(\displaystyle{ t=0 }\)。
\(\begin{align*} \frac{A(0)}{B(0)} &= \frac{12{ {e}^{-0.009\times 0}}}{3{ {e}^{-0.003\times 0}}} \\ &= 4 \end{align*}\)
所以,\(A\) 與 \(B\) 最初的質量比是 \(\displaystyle{ 4:1 }\)。
(2) \(\displaystyle{100 }\) 年後,即 \(\displaystyle{ t=100 }\)。
\(\begin{align*} \frac{A(100)}{B(100)} &= \frac{12{ {e}^{-0.009\times 100}}}{3{ {e}^{-0.003\times 100}}} \\ &= 4{ {e}^{-0.6}} \\ & \approx 2.2 \end{align*}\)
所以,\(A\) 與 \(B\) 在 \(\displaystyle{ 100 }\) 年後的質量比是 \(\displaystyle{ 2.2:1 }\)。