\(16\) 世紀末至 \(17\) 世紀初的時候,當時在自然科學領域(特別是天文學)的發展上,經常遇到大量精密又龐大的數值計算,於是數學家們為了尋求化簡的計算方法而發明了對數。
對數計算的功能在於將數值較大的兩數之乘法、除法或冪運算轉化為對數的加法、減法和乘法的運算來處理,使某些繁難的計算成為可能。在發明電子計算機之前,對數在冗長的數值運算中是很有用的,對科學進步有著具大的貢獻,尤其是天文學,並廣泛運用於工程、航海和測繪等領域中。

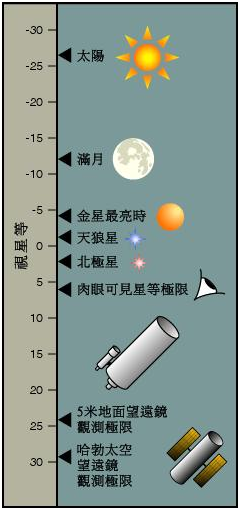
星等是衡量天體光度的量,由古希臘天文學家 Hipparchus 於公元二世紀時提出。星等的數值越小,星星越亮;反之,星等值越大,星星越暗。星等數每相差 \(\displaystyle{ 1 }\),星的亮度大約相差 \(\displaystyle{ 2.5 }\) 倍。星等的計算方法便是利用對數。
根據星等的計算公式,天空中有一等星 \(\displaystyle{ 21 }\) 顆,二等星有 \(\displaystyle{ 46 }\) 顆,三等星 \(\displaystyle{ 134 }\) 顆,四等星共 \(\displaystyle{ 458 }\) 顆,五等星有 \(\displaystyle{ 1476 }\) 顆,六等星共 \(\displaystyle{ 4840 }\) 顆,共計 \(\displaystyle{ 6974 }\) 顆。
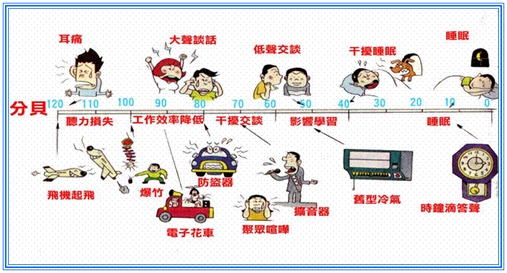
分貝 (decibel) 是一種測量聲音強度的單位,常用 \(\rm{dB}\) 表示。它的計算依賴於功率量和場量的不同,用對數標度來表達,從而讓極大或極小的聲音都可以用簡單的數字表示。
例如普通呼吸聲音大約是 \(\displaystyle{ 10 }\) \(\rm{dB}\),一般舒適的交談聲音大約是 \(\displaystyle{ 60 }\) \(\rm{dB}\),而噴氣式飛機起飛的聲音將達到 \(\displaystyle{ 140 }\) \(\rm{dB}\),影響人的聽力,容易讓人惡心。
用對數標度來表達聲音還有另一優點,就是人類的聽覺反應是基於聲音的相對變化而非絕對的變化,對數標度正好能模仿人類耳朵對聲音的反應。
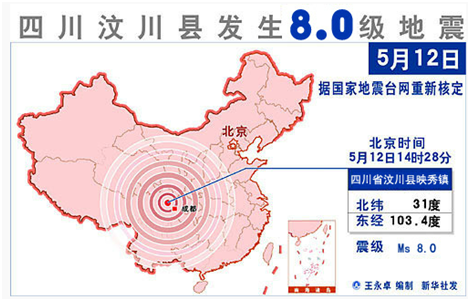
至 \(2008\) 年起,近五年內,我國發生 \(\displaystyle{ 6.0 }\) 級以上的地震超過十次,其中最嚴重的就是 \(2008\) 年 \(5\) 月 \(12\) 日四川省汶川縣發生的大地震,地震造成 \(\displaystyle{ 69227 }\) 人遇難,\(\displaystyle{ 374643 }\) 人受傷,\(\displaystyle{ 17923 }\) 人失踪。此次地震是新中國成立以來,國內破壞性最強、波及範圍最廣的地震,也是既 \(1976\) 年河北省唐山大地震後傷亡最慘重的一次。
為了表示地震的規模大小,國際上統一使用由兩位來自美國加州理工學院的地震學家黎克特和古騰堡,於 \(1935\) 年共同制定的黎克特制地震震級的量度制度。 此制度是根據觀測點處地震儀所記錄到的地震波最大振幅的常用對數演算而來。
根據黎克特制,汶川地震的強度達到 \(\displaystyle{ 8.0 }\) 級, 唐山大地震的震級則是 \(\displaystyle{ 7.8 }\) 級,而歷史紀錄中最強烈的地震是 \(1960\) 年 \(5\) 月 \(22\) 日的智利大地震,震級為 \(\displaystyle{ 9.5 }\)。 此地震度量標度,方便人們容易區別地震的大小。例如 \(4\) 級以下的地震一般不會造成明顯的破壞,而 \(\displaystyle{ 6 }\) 級以上的地震都是屬於較強威力的地震。
對數的定義:若 \(\displaystyle{{{a}^{x}}=b }\) (\(\displaystyle{ a \gt 0 }\) 且 \(\displaystyle{a\ne 1 }\)),則 \(\displaystyle{ x }\) 稱為以 \(\displaystyle{ a }\) 為底 \(\displaystyle{ b }\) 的對數 (Logarithm),記作 \(\displaystyle{{{\log }_{a}}b=x }\)。
例如:\(\displaystyle{{{10}^{8}}=100,000,000 }\),則 \(\displaystyle{{{\log }_{10}}100,000,000=8 }\)。對數的存在極大地化簡了大數的規模。
當 \(\displaystyle{ a = 10 }\) 時,\(\displaystyle{{{\log }_{10}}b }\) 稱為常用對數,簡寫為 \(\displaystyle{logb }\)。
當 \(\displaystyle{ a = e }\) 時,\(\displaystyle{{{\log }_{e}}b }\) 稱為自然對數,簡寫為 \(\displaystyle{lnb }\)。
同指數一樣,對數的底 \(\displaystyle{ a }\) 是不等於 \(\displaystyle{ 1 }\) 的正數。之後涉及對數時,均默認底為不等於 \(\displaystyle{ 1 }\) 正數。
注意:當 \(\displaystyle{ b \le 0 }\) 時,\(\displaystyle{{{\log }_{a}}b }\) ( \(\displaystyle{ a \gt 0 }\) 且 \(\displaystyle{ a\ne 1 }\) ) 在實數範圍內是不存在的。
因為 \(\displaystyle{x={{\log }_{a}}b }\),則 \(\displaystyle{{{a}^{x}}=b }\)。任何正數的指數都大於零,所以 \(\displaystyle{{{a}^{x}}=b\le 0 }\) 無實解,即使得 \(\displaystyle{{{a}^{x}}\le 0 }\) 的實數 \(\displaystyle{ x }\) 不存在。
在十五世紀歐洲文藝復興時期,遠洋運輸工業迅速發展,常常涉及到一些複雜且冗長的大數目的數學運算。
\(1484\) 年,法國數學家 Nicolas Chuquet 發現了關於等比數列和等差數列的有趣數學問題:
| 等比數列 \(\rm{A}\) | \(\displaystyle{ {{r}^{0}} }\) | \(\displaystyle{ {{r}^{1}} }\) | \(\displaystyle{ {{r}^{2}} }\) | \(\displaystyle{ {{r}^{3}} }\) | \(\displaystyle{ {{r}^{4}} }\) | \(\displaystyle{… … }\) | \(\displaystyle{ {{r}^{n}} }\) | \(\displaystyle{ … … }\) |
|---|---|---|---|---|---|---|---|---|
| 等差數列 \(\rm{B}\) | \(\displaystyle{ 0 }\) | \(\displaystyle{ 1 }\) | \(\displaystyle{ 2 }\) | \(\displaystyle{ 3 }\) | \(\displaystyle{ 4 }\) | \(\displaystyle{ … … }\) | \(\displaystyle{ n }\) | \(\displaystyle{ … … }\) |
根據以上關係,如果要找出數列 \(\rm{A}\) 中任意兩個數之積,可以先找出數列 \(\rm{B}\) 中與該兩個數對應的數之和 \(\displaystyle{ s }\),在找出 \(\displaystyle{ s }\) 在數列 \(\rm{A}\) 中對應的數字,即為答案,這種方法大大地簡化計算程序。
其後,德國數學家 Michael Stifel 將以上關係擴展至負指數和有理數指數,使得該計算方法得到更廣泛的應用。
蘇格蘭數學家 John Napier 亦利用上述思想,提出了對數的概念,對數的提出大大減少極大數值的計算。 他花了二十年的時間編制了一個準確至七位有效數字的對數表。

\(1622\) 年,Willian Oughtred 發明了對數尺,用來計算對數的加法、減法和乘法。對數尺成為當時科學界和工程界中最常用的對數計算工具。
時至今日,由於科學計算器和電腦的迅速發展,前人所製作的對數表和對數尺已很少人採用,電子計算機已成為計算對數最方便的工具。
![By ArnoldReinhold (Own work) [CC BY-SA 2.5]](img/L1_6.png)