對數與指數的關係：若 \(\displaystyle{{{a}^{x}}=b }\)，則 \(\displaystyle{x={{\log }_{a}}b }\)，即對數是指數的逆運算。
根據此關係，可得到對數的以下性質。
| 性質 1：\(\displaystyle{{{\log }_{a}}a=1 }\) |
由指數性質 \(\displaystyle{{{a}^{1}}=a }\) 得到
|
|
| 性質 2：\(\displaystyle{{{\log }_{a}}1=0 }\) |
由指數性質 \(\displaystyle{{{a}^{0}}=1 }\) 得到
|
|
| 性質 3：\(\displaystyle{{{\log }_{a}}\left( {{a}^{b}} \right)=b }\) |
由恆等式 \(\displaystyle{{{a}^{b}}={{a}^{b}} }\) 得到
|
|
| 性質 4：\(\displaystyle{{{a}^{{{\log }_{a}}b}}=b }\) |
由恆等式 \(\displaystyle{{{\log }_{a}}b={{\log }_{a}}b }\) 得到
|
例題：計算 \(\displaystyle{{{\log }_{5}}625 }\) 的值。
解：根據性質 3 求解。
\(\displaystyle{{{\log }_{5}}625={{\log }_{5}}{{5}^{4}}=4 }\)
對數的運算法則可由已學習的指數運算法則推導出來。
以下的運算法則用常數對數 \(\displaystyle{ log }\) 表示，該運算法則適用於任何以非 \(\displaystyle{ 1 }\) 的正數為底的對數。
| (1) \(\displaystyle{ \log x+\log y=\log xy }\) |
推導 1：令 \(\displaystyle{x={{a}^{p}} }\)，\(\displaystyle{y={{a}^{q}} }\)，則：\(\displaystyle{p={{\log }_{a}}x }\)，\(\displaystyle{q={{\log }_{a}}y }\)
由指數法則可得：\(\displaystyle{xy={{a}^{p}}\times {{a}^{q}}={{a}^{p+q}} }\) 則：\(\displaystyle{{{\log }_{a}}xy=p+q={{\log }_{a}}x+{{\log }_{a}}y }\) |
|||||||
| (2) \(\displaystyle{\log x-\log y=\log \frac{x}{y} }\) |
推導 2：令 \(\displaystyle{x={{a}^{p}} }\)，\(\displaystyle{y={{a}^{q}} }\)，則：\(\displaystyle{p={{\log }_{a}}x }\)，\(\displaystyle{q={{\log }_{a}}y }\)
由指數法則可得：\(\displaystyle{\frac{x}{y}={{a}^{p}}\div {{a}^{q}}={{a}^{p-q}} }\) 則：\(\displaystyle{{{\log }_{a}}\frac{x}{y}=p-q={{\log }_{a}}x-{{\log }_{a}}y }\) |
|||||||
| (3) \(\displaystyle{n\log x=\log {{x}^{n}} }\) |
推導 3：令 \(\displaystyle{x={{a}^{p}} }\)，則：\(\displaystyle{p={{\log }_{a}}x }\)
由指數法則可得：\(\displaystyle{{{x}^{n}}={{\left( {{a}^{p}} \right)}^{n}}={{a}^{pn}} }\) 則：\(\displaystyle{{{\log }_{a}}{{x}^{n}}=np=n{{\log }_{a}}x }\) |
|||||||
|
根據以上三個運算法則，注意：
|
||||||||
| (4) \(\displaystyle{\log \frac{1}{x}=-\log x }\) |
推導 4：根據運算法則 (3)，令 \(\displaystyle{ n=-1 }\)，則可以得到該運算法則。
|
|||||||
| (5) 換底公式：\(\displaystyle{{{\log }_{a}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}a} }\) |
推導 5：令 \(\displaystyle{x={{\log }_{a}}b }\)，則 \(\displaystyle{b={{a}^{x}} }\) 根據換底公式，可以推導出 (6) ~ (8) 的運算規則： |
|||||||
| (6) \(\displaystyle{{{\log }_{a}}b=\frac{1}{{{\log }_{b}}a} }\) |
推導 6：根據換底公式 (5)，令 \(\displaystyle{ c=b }\)，即可以得到該運算法則。
|
|||||||
| (7) \(\displaystyle{{{\log }_{{{a}^{r}}}}b=\frac{1}{r}{{\log }_{a}}b }\) |
推導 7：根據換底公式 (5)得：
\(\displaystyle{{{\log }_{{{a}^{r}}}}b=\frac{{{\log }_{c}}b}{{{\log }_{c}}{{a}^{r}}}=\frac{{{\log }_{c}}b}{r{{\log }_{c}}a}=\frac{1}{r}\cdot \frac{{{\log }_{c}}b}{{{\log }_{c}}a} }\) 再根據換底公式得：\(\displaystyle{{{\log }_{{{a}^{r}}}}b=\frac{1}{r}{{\log }_{a}}b }\) |
|||||||
| (8) \(\displaystyle{{{\log }_{{{a}^{r}}}}{{b}^{s}}=\frac{s}{r}{{\log }_{a}}b }\) |
推導 8：根據換底公式 (5)得：
\(\displaystyle{{{\log }_{{{a}^{r}}}}{{b}^{s}}=\frac{{{\log }_{c}}{{b}^{s}}}{{{\log }_{c}}{{a}^{r}}}=\frac{s{{\log }_{c}}b}{r{{\log }_{c}}a}=\frac{s}{r}\cdot \frac{{{\log }_{c}}b}{{{\log }_{c}}a} }\) 再根據換底公式得：\(\displaystyle{{{\log }_{{{a}^{r}}}}{{b}^{s}}=\frac{s}{r}{{\log }_{a}}b }\) |
|||||||
例 1：簡化以下表達式。
(1) \(\displaystyle{{{\log }_{2}}5+\frac{1}{2}{{\log }_{2}}36-{{\log }_{2}}10 }\)
(2) \(\displaystyle{{{\log }_{2}}ab+\frac{1}{2}{{\log }_{2}}{{a}^{2}}{{b}^{3}}-{{\log }_{2}}\frac{\sqrt{b}}{{{a}^{2}}} }\)
解：
\(\begin{align*}(1) \ & {{\log }_{2}}5+\frac{1}{2}{{\log }_{2}}36-{{\log }_{2}}10 \\ &= {{\log }_{2}}\left( 5\times {{36}^{\frac{1}{2}}}\div 10 \right) \\ &= {{\log }_{2}}3 \end{align*}\)
\(\begin{align*}(2) \ & {{\log }_{2}}ab+\frac{1}{2}{{\log }_{2}}{{a}^{2}}{{b}^{3}}-{{\log }_{2}}\frac{\sqrt{b}}{{{a}^{2}}} \\ &= {{\log }_{2}}\left[ \left( ab \right)\times {{\left( {{a}^{2}}{{b}^{3}} \right)}^{\frac{1}{2}}}\div \left( {{b}^{\frac{1}{2}}}{{a}^{-2}} \right) \right] \\ &= 2{{\log }_{2}}{{a}^{2}}b \end{align*}\)
例 2：若 \(\displaystyle{{{\log }_{2}}3=a }\)，\(\displaystyle{{{\log }_{3}}7=b }\)，試以 \(\displaystyle{ a }\)、\(\displaystyle{ b }\) 表示 \(\displaystyle{{{\log }_{63}}84 }\)。
提示：運用換底公式 （ 換任何底，結果是一樣的 ）。
方法一：運用換底公式，換成以 \(\displaystyle{ 2 }\) 為底的對數。
\(\begin{align*} {{\log }_{63}}84 &= \frac{{{\log }_{2}}84}{{{\log }_{2}}63} \\ &= \frac{{{\log }_{2}}2\times 2\times 3\times 7}{{{\log }_{2}}7\times 3\times 3} \\ &= \frac{{{\log }_{2}}2+{{\log }_{2}}2+{{\log }_{2}}3+{{\log }_{2}}7}{{{\log }_{2}}7+{{\log }_{2}}3+{{\log }_{2}}3} \end{align*}\)
\(\begin{align*} {{\log }_{2}}7 &= \frac{{{\log }_{3}}7}{{{\log }_{3}}2} \\ &= {{\log }_{3}}7\times {{\log }_{2}}3 \\ &= ab \end{align*}\)
\(\displaystyle{\therefore {{\log }_{63}}84=\frac{ab+a+2}{ab+2a} }\)
方法二：運用換底公式，換成以 \(\displaystyle{ 3 }\) 為底的對數。
\(\begin{align*} {{\log }_{63}}84 &= \frac{{{\log }_{3}}84}{{{\log }_{3}}63} \\ &= \frac{{{\log }_{3}}2\times 2\times 3\times 7}{{{\log }_{3}}7\times 3\times 3} \\ &= \frac{{{\log }_{3}}2+{{\log }_{3}}2+{{\log }_{3}}3+{{\log }_{3}}7}{{{\log }_{3}}7+{{\log }_{3}}3+{{\log }_{3}}3} \\ &= \frac{{}^{1}\!\!\diagup\!\!{}_{{{\log }_{2}}3}\;+{}^{1}\!\!\diagup\!\!{}_{{{\log }_{2}}3}\;+{{\log }_{3}}3+{{\log }_{3}}7}{{{\log }_{3}}7+{{\log }_{3}}3+{{\log }_{3}}3} \\ &= \frac{\frac{1}{a}+\frac{1}{a}+1+b}{b+2} \\ &= \frac{ab+a+2}{ab+2a} \end{align*}\)
計算機為對數只提供常數對數和自然對數的計算按鍵
和 
，運用換底公式，可以將以任何數為底的對數 \(\displaystyle{{{\log }_{a}}b }\) 轉換成常用對數或自然對數。
\[\displaystyle{{{\log }_{a}}b=\frac{\ln b}{\ln a}=\frac{\log b}{\log a} }\]
無論用按鍵 或，得到的結果值是一樣的。
求對數 \(\displaystyle{{{\log }_{a}}b }\) 的按鍵次序：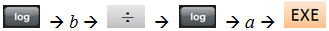
；
或者：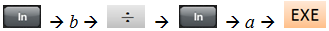
。