許多數學模型都涉及連續增長或衰退的概念,增長或衰退的程度取決於原本數量的大小、增長或衰退的速率以及持續的時間,這些模型常應用在生物、物理、經濟生活等方面。
以下列舉了一些常見的例子,請同學回答相應的問題。
世界上的生物各式各樣,由小變大,不斷生長成熟,就像一個剛出生、只有數磅重的嬰兒,不斷發展成長為超過一百磅的成人,這依賴於細胞的分裂增殖。細胞分裂是生物體生長、發育和繁殖的基礎,如視頻所示,它是一個細胞分裂為兩個細胞的過程。分裂前的細胞稱母細胞,分裂後形成的新細胞稱子細胞。
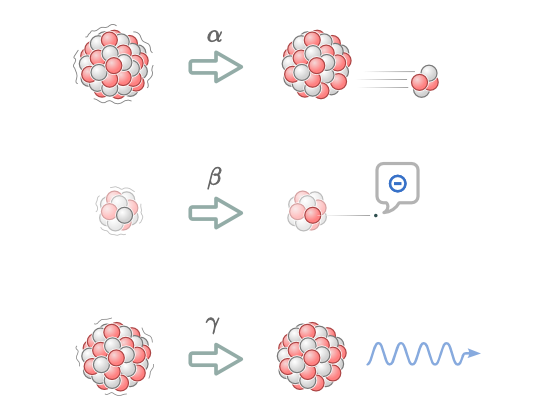
放射性元素能夠自發地從不穩定的原子核內部放出粒子或射線 (如 \(\displaystyle{\alpha }\) 射線、\(\displaystyle{\beta }\) 射線、\(\displaystyle{\gamma }\) 射線等),同時釋放出能量,最終衰變形成穩定的元素而停止放射。每種放射性元素都有半衰期,經過半衰期後,其濃度降低至初始時的一半。放射性元素的半衰期常常用來測定年代。
例如,碳 \(\displaystyle{ (C) }\) 是有機物的元素之一,生物體在活著的時候會因呼吸、進食等不斷的從外界攝入放射性元素碳十四 \(\displaystyle{ (C14) }\),最終體內碳十四 \(\displaystyle{ (C14) }\) 與碳十二 \(\displaystyle{ (C12) }\) 的比值會達到與環境一致;當生物體死亡時,碳十四 \(\displaystyle{ (C14) }\) 的攝入停止,之後因遺體中碳十四 \(\displaystyle{ (C14) }\) 的衰變,使遺體中的碳十四 \(\displaystyle{ (C14) }\) 與碳十二 \(\displaystyle{ (C12) }\) 比值發生變化,通過測定殘餘碳十四 \(\displaystyle{ (C14) }\) 與碳十二 \(\displaystyle{ (C12) }\) 的比值就可以推斷該生物的死亡年代,這就是古生物學中常用的碳十四 \(\displaystyle{ (C14) }\) 測年法。
複利是一種計算利息常用的方法,按照這種方法,計算每期末之利息,是以前一期末所得之本金加利息的和作為下期本金,即除了根據本金計算外,新得到的利息同樣可以生息。

以上關於生物學、物理學及經濟學方面的知識都涉及到數學中的指數,這些數據呈現出指數性的增長或減少。
指數 (Exponent)在數學中代表次方,也叫做 「冪」,表示幾個相同因數相乘的關係。其基本形式為 \(\displaystyle{{{a}^{n}} }\),表示 \(\displaystyle{ n }\) 個 \(\displaystyle{ a }\) 相乘的積,即
\[\displaystyle{{{a}^{n}}=\overbrace{a\times a\times a\times \cdots \times a}^{n} }\]其中 \(\displaystyle{ a }\) 叫做底,\(\displaystyle{ n }\) 叫做指數。當 \(\displaystyle{ n }\) 是整數時,該指數稱為整數指數。
例如,\(\displaystyle{{{2}^{4}} }\) 表示 \(\displaystyle{2\times 2\times 2\times 2 }\),其中 \(\displaystyle{ 2 }\) 是底數,\(\displaystyle{ 4 }\) 是指數。
注意:\(\displaystyle{{{a}^{1}}=a }\)。