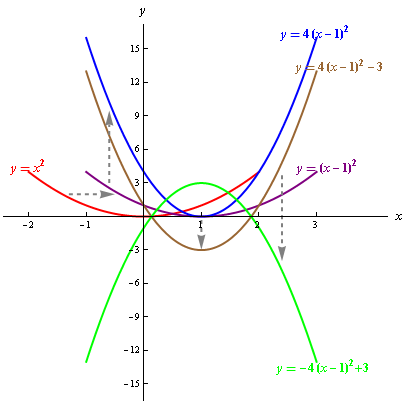
請描述函數 \(\displaystyle{f\left( x \right)={{x}^{2}} }\) 的圖像變換至函數 \(\displaystyle{g\left( x \right)=-4{{\left( x-1 \right)}^{2}}+3 }\) 的圖像的方式。
解:函數 \(\displaystyle{ f\left( x \right) }\) 的圖像可以由函數 \(\displaystyle{ g\left( x \right) }\) 的圖像經平移、伸縮、反射變換後得到。
變換方式,如圖 \(1\) 所示:
將函數 \(\displaystyle{f\left( x \right)={{x}^{2}} }\) 的圖像 (紅色曲綫) 右移 \(\displaystyle{1 }\) 個單位,得到函數 \(\displaystyle{y={{\left( x-1 \right)}^{2}} }\) 的圖像 (紫色曲綫);
將函數 \(\displaystyle{y={{\left( x-1 \right)}^{2}} }\) 的圖像 (紫色曲綫) 沿鉛垂方向放大至 \(\displaystyle{ 4 }\) 倍,得到函數 \(\displaystyle{y=4{{\left( x-1 \right)}^{2}} }\) 的圖像 (藍色曲綫);
將函數 \(\displaystyle{y=4{{\left( x-1 \right)}^{2}} }\) 的圖像 (藍色曲綫) 沿 \(\displaystyle{ x }\) 軸反射,得到函數 \(\displaystyle{y=-4{{\left( x-1 \right)}^{2}} }\) 的圖像 (橘色曲綫);
將函數 \(\displaystyle{y=-4{{\left( x-1 \right)}^{2}} }\) 的圖像 (橘色曲綫) 上移 \(\displaystyle{ 3 }\) 個單位,最終可得到函數 \(\displaystyle{g\left( x \right)=-4{{\left( x-1 \right)}^{2}}+3 }\) 的圖像 (綠色曲綫)。
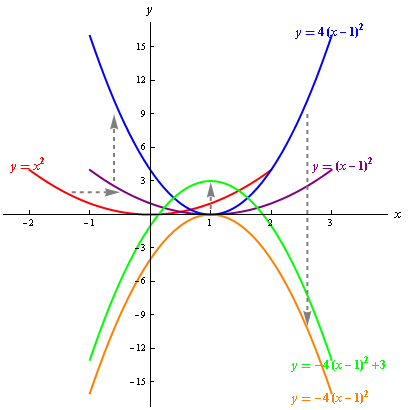
思考 \(1\):函數 \(\displaystyle{ g\left( x \right) }\) 的圖像可以由函數 \(\displaystyle{ f\left( x \right) }\) 的圖像經以上四步的變換得到,那麼以上的步驟的次序是否可以互換呢?
思考 \(1\):函數 \(\displaystyle{ g\left( x \right) }\) 的圖像可以由函數 \(\displaystyle{ f\left( x \right) }\) 的圖像經以上四步的變換得到,那麼以上的步驟的次序是否可以互換呢?
解答:可以。如圖 \(2\) 所示,將上述四步變換的第一步 (平移) 和第二步 (伸縮) 的順序交換:
將函數 \(\displaystyle{f\left( x \right)={{x}^{2}} }\) 的圖像 (紅色曲綫) 沿鉛垂方向放大至 \(\displaystyle{ 4 }\) 倍,得到函數 \(\displaystyle{y=4{{x}^{2}}}\) 的圖像 (深黃色曲綫);
將函數 \(\displaystyle{y=4{{x}^{2}} }\) 的圖像 (深黃色曲綫) 右移 \(\displaystyle{ 1 }\) 個單位,得到函數 \(\displaystyle{y=4{{\left( x-1 \right)}^{2}} }\) 的圖像 (藍色曲綫);
步驟 (3) 和步驟 (4) 與圖 1 的變換方式相同,最終也可以得到函數 \(\displaystyle{g\left( x \right)=-4{{\left( x-1 \right)}^{2}}+3 }\) 的圖像 (綠色曲綫)。
交換圖 \(1\) 表示的變換方式之第一步的平移和第二步的伸縮,同樣可得函數 \(\displaystyle{ g\left( x \right) }\) 的圖像。
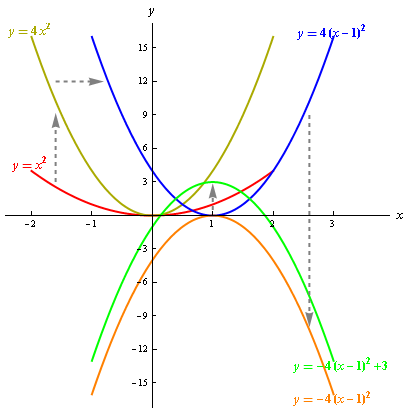
思考 \(2\):是不是在函數變換時,任意交換變換的次序將不會影響變換後的結果呢?
思考 \(2\):在函數變換時,任意交換變換的次序是否不會影響變換後的結果?
解答:不是。變換次序的交換常常產生不同的變換結果。
例如將圖 \(1\) 中變換方式的第三步 (反射) 和第四步 (平移) 交換,得到的圖像不再代表函數 \(\displaystyle{ g\left( x \right) }\),如圖 \(3\) 所示,得到的圖像是函數 \(\displaystyle{y=-4{{\left( x-1 \right)}^{2}}-3 }\) 的圖像。
步驟 (1) 和步驟 (2) 不變,與圖 \(1\) 的變換方式相同。
(3) 將函數 \(\displaystyle{y=4{{\left( x-1 \right)}^{2}} }\) 的圖像 (藍色曲綫) 上移 \(\displaystyle{ 3 }\) 個單位,得到函數 \(\displaystyle{y=4{{\left( x-1 \right)}^{2}}+3 }\) 的圖像 (粉色曲綫);
(4) 將函數 \(\displaystyle{y=4{{\left( x-1 \right)}^{2}}+3 }\) 的圖像 (粉色曲綫) 沿 \(\displaystyle{ x }\) 軸反射,最終可得到函數 \(\displaystyle{y=-4{{\left( x-1 \right)}^{2}}-3 }\) 的圖像 (黑色曲綫)。
此黑色曲綫與綠色虛線所代表的函數 \(\displaystyle{g\left( x \right) }\) 的曲綫不相同。
因此,交換函數變換次序會得到不同的函數圖像。
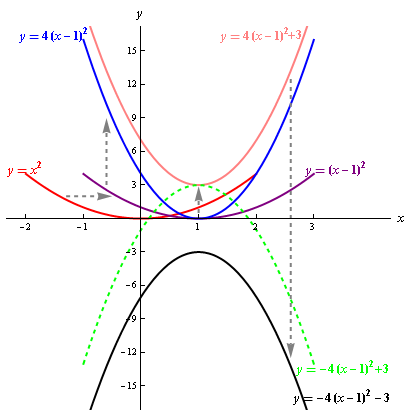
如果需要交換圖 \(1\) 中變換方式的第三步 (反射) 和第四步 (平移) 的變換,並且最終也得到函數 \(\displaystyle{g\left( x \right) }\) 的圖像,只需要對平移作出些許改動即可實現。
步驟 (1) 和步驟 (2) 不變,與圖 \(4.1\) 的變換方式相同。
(3) 將函數 \(\displaystyle{y=4{{\left( x-1 \right)}^{2}} }\) 的圖像下移 \(\displaystyle{ 3 }\) 個單位,得到函數 \(\displaystyle{y=4{{\left( x-1 \right)}^{2}}-3 }\) 的圖像 (棕色曲綫);
(4) 將函數 \(\displaystyle{y=4{{\left( x-1 \right)}^{2}}-3 }\) 的圖像 (棕色曲綫)沿 \(\displaystyle{ x }\) 軸反射,得到函數 \(\displaystyle{g\left( x \right)=-4{{\left( x-1 \right)}^{2}}+3 }\) 的圖像 (綠色曲綫)。
函數的變換次序會影響到變換的結果,需靈活運用。