該實驗以常見的三個函數 \(f(x)\) 為例,包括二次函數、多項式函數和指數函數,展示了函數 \(f(x)\)、\(\displaystyle{ p f\left( x \right) }\) 與 \(\displaystyle{ f\left(q x \right) }\) 的圖像。請選擇不同的函數,改變 \(p\) 與 \(q\) 的數值,比較三條曲線在直角坐標系中的位置關係。
在此,只考慮 \(\displaystyle{ p \gt 0 }\) 和 \(\displaystyle{ q \gt 0 }\) 的情況,\(\displaystyle{ p \lt 0 }\) 與 \(\displaystyle{ q \lt 0 }\) 的情況可以根據函數的反射法則推導。
如模擬程式所示,任意一條鉛垂線與函數 \(f(x)\) 和函數 \(\displaystyle{ p f\left( x \right) }\) 分別交於 \(A\) 點和 \(B\) 點,任意一條水平線與函數 \(f(x)\) 和函數 \(\displaystyle{ f\left( qx \right) }\) 分別交於 \(C\) 點和 \(D\) 點。選擇不同的函數,改變 \(\displaystyle{ p }\) 和 \(\displaystyle{ q }\) 的值,移動各曲線上的點,觀察\(A\) 點和 \(B\) 點到 \(\displaystyle{ x}\) 軸的距離的變化,以及 \(C\) 點和 \(D\) 點到 \(\displaystyle{ y }\) 軸的距離的變化。
函數 \(\displaystyle{f\left( x \right) }\)、\(\displaystyle{ pf\left( x \right) }\) 與 \(\displaystyle{ f\left( qx \right) }\) 三者圖像的形狀是否相同?
根據以上數學實驗的實驗結果,我們可總結出函數的伸縮法則:
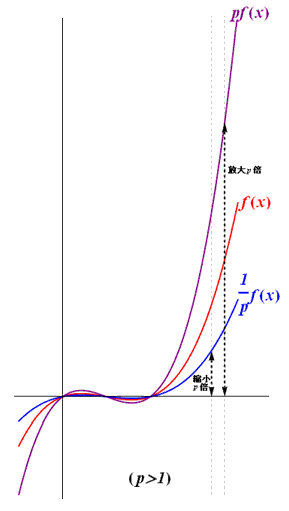
鉛垂方向伸縮
函數 \(\displaystyle{ p f\left( x \right) \left( p \gt 0 \right) }\) 的圖像可由函數 \(\displaystyle{f\left( x \right) }\) 的圖像沿鉛垂方向伸縮 \(\displaystyle{ p }\) 倍得到。 當 \(\displaystyle{ p \gt 1 }\) 時,函數 \(\displaystyle{f\left( x \right) }\) 沿此方向放大得到函數 \(\displaystyle{ p f\left( x \right) }\); 當 \(\displaystyle{ 0 \lt p \lt 1 }\) 時,函數 \(\displaystyle{f\left( x \right) }\) 沿此方向縮小得到函數 \(\displaystyle{ p f\left( x \right) }\)。
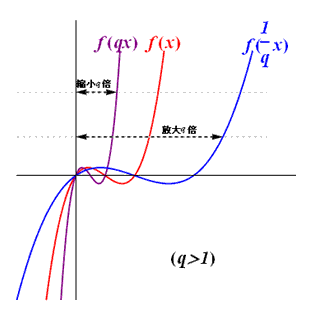
水平方向伸縮
函數 \(\displaystyle{ f\left( qx \right) \left( q \gt 0 \right) }\) 的圖像可由函數 \(\displaystyle{f\left( x \right) }\) 的圖像沿水平方向伸縮 \(\displaystyle{ q }\) 倍得到。 當 \(\displaystyle{ q \gt 1 }\) 時,函數 \(\displaystyle{f\left( x \right) }\) 沿此方向縮小得到函數 \(\displaystyle{ f\left( qx \right) }\); 當 \(\displaystyle{ 0 \lt q \lt 1 }\) 時,函數 \(\displaystyle{f\left( x \right) }\) 沿此方向放大得到函數 \(\displaystyle{ f\left( qx \right) }\)。
法則補充:
\(\displaystyle{ p \lt 0 }\) 的情況:先根據函數 \(\displaystyle{ p f\left( x \right) \left( p \gt 0 \right) }\) 的圖像沿鉛垂方向的伸縮法則得到 \(\displaystyle{\left| p \right|\cdot f\left( x \right) }\) 的圖像, 再將所得函數圖像沿 \(\displaystyle{ x }\) 軸反射即可得到函數 \(\displaystyle{ p f\left( x \right) }\) 的圖像。
\(\displaystyle{ q \lt 0 }\) 的情況:先根據函數 \(\displaystyle{ f\left( qx \right) \left( q \gt 0 \right) }\) 的圖像沿水平方向的伸縮法則得到 \(\displaystyle{ f\left( \left| q \right|\cdot x \right) }\) 的圖像, 再將所得函數圖像沿 \(\displaystyle{ y }\) 軸反射即可得到函數 \(\displaystyle{ f\left( qx \right) }\) 的圖像。
思考:調換函數 \(\displaystyle{ f\left( x \right) }\) 沿水平方向和鉛垂方向伸縮的順序,即將函數 \(\displaystyle{ f\left( x \right) }\) 的圖像先沿水平方向縮小至 \(\displaystyle{ 0.25 }\) 倍,再沿鉛垂方向放大至 \(\displaystyle{ 2 }\) 倍,是否也可得到函數 \(\displaystyle{ g\left( x \right) }\) 的圖像?