在之前的課堂中,我們已學會直線的方程及兩條直線相交的各種情況。這一節我們會探討它們在幾何問題,特別是三角形中心點上的應用。
三角形的中線(median)是從一頂點到對邊中點的直線。一個三角形有三條中線,它們相交於一點,稱為三角形的形心(centroid)。
例子:如圖中所示,三角形\(\;\triangle ABC\;\)的頂點分別為\(\;A(-8,-8)\)、\(B(-2,6)\;\)和\(\;C(7,-4)\),點\(\;D\)、\(E\)、\(F\;\)分別為\(\;BC\)、\(AC\)、\(AB\;\)的中點。求這三角形形心的坐標。
形心是中線的交點,所以我們先找出其中兩條中線的方程。點\(\;D\;\)的坐標為\(\;\displaystyle \left( \frac{-2+7}{2}, \frac{6+(-4)}{2} \right) = \left( \frac{5}{2}, 1 \right)\),所以中線\(\;AD\;\)的方程為
\begin{align} \frac{y-(-8)}{x-(-8)} &= \frac{1-(-8)}{\frac{5}{2}-(-8)} \nonumber \\ \frac{y+8}{x+8} &= \frac{6}{7} \nonumber \\ 7y+56 &= 6x+48 \nonumber \\ 6x-7y-8 &= 0 \label{eqn11} \end{align}同樣地,點\(\;E\;\)的坐標為\(\;\displaystyle \left( \frac{-8+7}{2}, \frac{-8+(-4)}{2} \right) = \left( -\frac{1}{2}, -6 \right)\),所以中線\(\;BE\;\)的方程為
\begin{align} \frac{y-6}{x-(-2)} &= \frac{-6-6}{-\frac{1}{2}-(-2)} \nonumber \\ \frac{y-6}{x+2} &= -8 \nonumber \\ y-6 &= -8x-16 \nonumber \\ y &= -8x-10 \label{eqn12} \end{align}把 \eqref{eqn12} 代入 \eqref{eqn11} 中,可得
\begin{align*} 6x - 7(-8x-10) -8 &= 0 \\ 62x + 62 &= 0 \\ x &= -1 \end{align*}代入 \eqref{eqn12} 中,得\(\;y=-8(-1)-10=-2\),所以\(\;\triangle ABC\;\)的形心坐標為\(\;(-1,-2)\)。
我們可以計算第三條中線\(\;CF\;\)的方程,並證明它也通過形心,詳情請按此。
設形心為\(\;O\),如果你還記得初中時學過
\begin{equation*} AO:OD = BO:OE = CO:OF = 2:1 \end{equation*}則我們可以截點公式來計算形心的坐標,這比找直線的交點簡單得多。
一般地,如果三角形的三個頂點是\(\;A(x_1,y_1)\)、\(B(x_2,y_2)\;\)和\(\;C(x_3,y_3)\),則形心的坐標為
\begin{equation*} \left( \frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3} \right) \end{equation*}這稱為形心公式,一般以第 2. 的方法來證明。
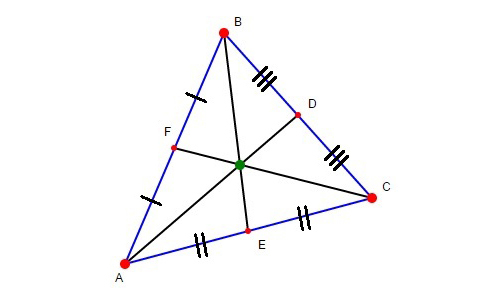
在右圖中,你可以隨意移動三角形的頂點\(\;A\)、\(B\)、\(C\),三角形的三條中線(黑線所示)和形心(綠點所示)的坐標將會自動顯示出來。試試移動頂點至不同位置,並觀察形心位置的變化。
形心在三角形之內還是外?
|
在三角形之內 |
在三角形之外 |
隨意移動頂點,你能找到一個三角形,其形心在三角形之外嗎?
|
能夠 |
不能夠 |
一個三角形的形心必定在三角形之內。請參看上面的例子來了解求形心坐標的方法。
在三角形的三條邊都畫一條垂直平分線,則它們相交於一點,稱為三角形的外心(circumcenter)。外心是三角形外接圓(circumcircle,即通過三角形三個頂點的那個圓)的圓心。
例子:如圖中所示,三角形\(\;\triangle ABC\;\)的頂點分別為\(\;A(-3,-7)\)、\(B(-9,5)\;\)和\(\;C(6,2)\),點\(\;D\)、\(E\)、\(F\;\)分別為\(\;BC\)、\(AC\)、\(AB\;\)的中點。求這三角形外心的坐標。
外心是三條邊的垂直平分線的交點,所以我們先找出其中兩條垂直平分線的方程。點\(\;D\;\)的坐標為\(\;\displaystyle \left( \frac{-9+6}{2}, \frac{5+2}{2} \right) = \left( -\frac{3}{2}, \frac{7}{2} \right)\),而\(\;BC\;\)的斜率為
\begin{equation*} BC \hbox{ 的斜率} = \frac{5-2}{-9-6} = -\frac{1}{5} \end{equation*}因此通過\(\;D\;\)點的垂直平分線的斜率為\(\;\displaystyle -1/(-\frac{1}{5}) = 5\),而其方程為
\begin{align} (y-\frac{7}{2}) &= 5(x-(-\frac{3}{2})) \nonumber \\ 2y-7 &= 10x+15 \nonumber \\ y &= 5x+11 \label{eqn21} \end{align}同樣地,點\(\;E\;\)的坐標為\(\;\displaystyle \left( \frac{-3+6}{2}, \frac{-7+2}{2} \right) = \left( \frac{3}{2}, -\frac{5}{2} \right)\),而\(\;AC\;\)的斜率為
\begin{equation*} AC \hbox{ 的斜率} = \frac{-7-2}{-3-6} = 1 \end{equation*}因此通過\(\;E\;\)點的垂直平分線的斜率為\(\;-1/1 = -1\),而其方程為
\begin{align} (y-(-\frac{5}{2})) &= (-1)(x-\frac{3}{2}) \nonumber \\ 2y+5 &= -2x+3 \nonumber \\ y &= -x-1 \label{eqn22} \end{align}把 \eqref{eqn22} 代入 \eqref{eqn21} 中,可得
\begin{align*} -x-1 &= 5x+11 \\ 6x &= -12 \\ x &= -2 \end{align*}代入 \eqref{eqn22} 中,得\(\;y=-(-2)-1=1\),所以\(\;\triangle ABC\;\)的外心坐標為\(\;(-2,1)\)。
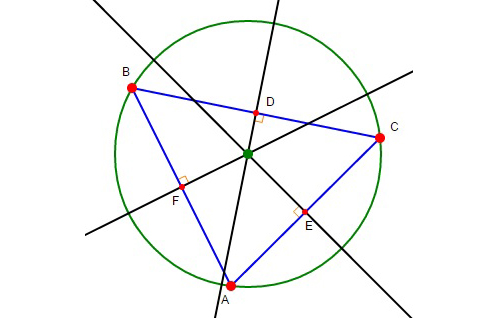
在右圖中,你可以隨意移動三角形的頂點\(\;A\)、\(B\)、\(C\),上述三條垂直平分線(黑線所示)和三角形的外心(綠點所示)的坐標將會自動顯示出來。試試移動頂點至不同位置,並觀察外心位置的變化。
移動三角形的頂點使三角形的所有角都是銳角。這時外心在三角形之內還是外?
|
在三角形之內 |
在三角形之外 |
現在,移動三角形的頂點使三角形的其中一隻角變成鈍角。這時外心在三角形之內還是外?
|
在三角形之內 |
在三角形之外 |
隨意移動頂點,你能找到一個三角形,其外心在三角形的一條邊上嗎?
|
能夠 |
不能夠 |
視乎三角形的種類,一個三角形的外心未必在三角形之內:
請參看上面的例子來了解求外心坐標的方法。
三角形的高線是從一頂點到對邊,並與該對邊垂直的直線。一個三角形有三條高線,它們相交於一點,稱為三角形的垂心(orthocenter)。
例子:如圖中所示,三角形\(\;\triangle ABC\;\)的頂點分別為\(\;A(-3,10)\)、\(B(-6,-8)\;\)和\(\;C(9,2)\)。求這三角形垂心的坐標。
垂心是三條高線的交點,所以我們先找出其中兩條高線的方程。首先,\(BC\;\)的斜率為
\begin{equation*} BC \hbox{ 的斜率} = \frac{2-(-8)}{9-(-6)} = \frac{2}{3} \end{equation*}因此通過\(\;A\;\)點的高線\(\;AF\;\)的斜率為\(\;\displaystyle -1/(\frac{2}{3}) = -\frac{3}{2}\),而其方程為
\begin{align} y-10 &= -\frac{3}{2}(x-(-3)) \nonumber \\ 2y-20 &= -3x-9 \nonumber \\ 3x+2y-11 &= 0 \label{eqn31} \end{align}同樣地,\(AC\;\)的斜率為
\begin{equation*} AC \hbox{ 的斜率} = \frac{10-2}{-3-9} = -\frac{2}{3} \end{equation*}因此通過\(\;B\;\)點的高線\(\;BE\;\)的斜率為\(\;\displaystyle -1/(-\frac{2}{3}) = \frac{3}{2}\),而其方程為
\begin{align} y-(-8) &= \frac{3}{2}(x-(-6)) \nonumber \\ 2y+16 &= 3x+18 \nonumber \\ 3x-2y+2 &= 0 \label{eqn32} \end{align}把 \eqref{eqn31} 和 \eqref{eqn32} 相加,可得
\begin{align*} 6x-9 &= 0 \\ x &= \frac{3}{2} \end{align*}把上式代入 \eqref{eqn32} 中,得
\begin{align*} 3(\frac{3}{2})-2y+2 &= 0 \\ 2y &= \frac{13}{2} \\ y &= \frac{13}{4} \end{align*}所以\(\;\triangle ABC\;\)的垂心坐標為\(\;\displaystyle (\frac{3}{2},\frac{13}{4})\)。
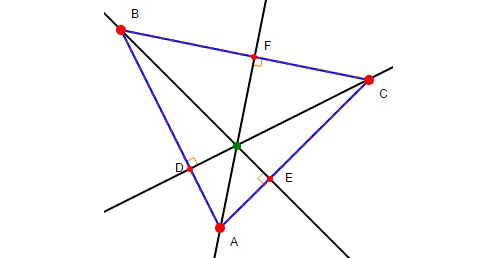
在右圖中,你可以隨意移動三角形的頂點\(\;A\)、\(B\)、\(C\),上述三條垂直平分線(黑線所示)和三角形的外心(綠點所示)的坐標將會自動顯示出來。試試移動頂點至不同位置,並觀察外心位置的變化。
移動三角形的頂點使三角形的所有角都是銳角。這時垂心在三角形之內還是外?
|
在三角形之內 |
在三角形之外 |
現在,移動三角形的頂點使三角形的其中一隻角變成鈍角。這時垂心在三角形之內還是外?
|
在三角形之內 |
在三角形之外 |
隨意移動頂點,你能找到一個三角形,其垂心在三角形的一條邊上嗎?
|
能夠 |
不能夠 |
視乎三角形的種類,一個三角形的外心未必在三角形之內:
請參看上面的例子來了解求垂心坐標的方法。