在進行統計調查時,選擇及正確地運用合適的抽樣數據收集和分折的方法是非常重要的。
誤用任何一種方法都可導到不正確的結論。
以下列舉一些利用統計把事實扭曲的例子。
利用「平均數」誤導讀者
例如,某間公司五位員工的月薪為
\(\qquad \qquad $8200 \; , \; $8700 \; , \; $9100 \; , \; $34000\)
則,
你覺得月薪\(\;\$12000\;\)能否很正確地反映出實際的狀況?
曲解百分數
例如,訪問員在一地鐵站中進行訪問。他們發覺已受訪問的八位乘客中,四位乘客使用八達通。
因此,他們聲稱\(\; 50 \%\;\)的地鐵乘客都選用八達通。
你覺得這說法能否很正確地反映出實際的狀況?
利用圖像對數據的誤示
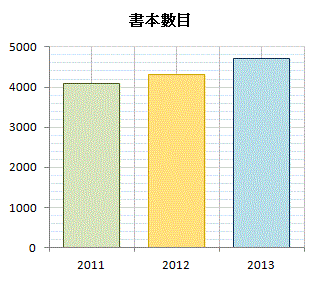
例如,下表所示為某一套教科書在過去三年售出的數目。
| \(\;\;\)年份 | \(2001\) | \(2002\) | \(2003\) |
|---|---|---|---|
| \(\;\;\)數目 | \(4100\) | \(4300\) | \(4700\) |
 \(\qquad\)
\(\qquad\)
 \(\qquad\)
\(\qquad\)
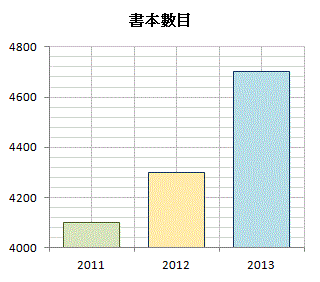
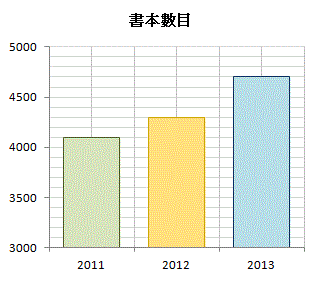
以上三個棒形圖均根據上表的數據畫出。為甚麼驟眼看來它們產生不同的效果?
雖然三個棒形圖均根據同一組的數據畫出,但它們所採用的標度並不同:
樣本欠缺代表性
例如,某百貨公司為了解顧客對其新裝修的意見,公司經理採用簡單隨機抽樣方法,從尊貴顧客名單中選出十個樣本,並進行電話訪問。
你覺得以這方法抽出樣本訪問能否很正確地反映出實際的狀況?
以這方法抽樣本,缺點如下:
在現實生活中,若所得的樣本欠缺代表性,便未必能夠完全反映總體的特性。
改善方法: 可在百貨公司的大門入口或在各部門派人,以簡單隨機抽樣選出適當數量的樣本。