在本課件,我們將討論更多有關圓切線與半徑的定理,及其計算方法。
定理 \(25\) 是定理 \(24\) (切線 \(\perp\) 半徑)的逆定理
|
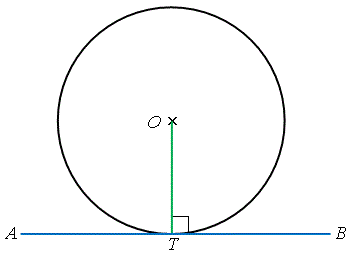
定理 \(25\)——切線 \(\perp\) 半徑的逆定理 設 \(OT\) 為圓的平徑,而 \(ATB\) 是一條直線。若 \(AB \perp OT\),則 \(AB\) 是圓於 \(T\) 點的切線。 |
|
綜合定理 \(24\) 和定理 \(25\),我們可以推論到以下定理。
|
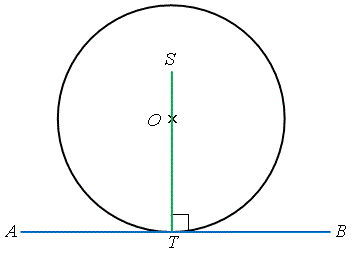
定理 \(26\)——垂直切線且通過切點的直線通過圓心 若 \(AB\) 為圓於 \(T\) 點的切線,且 \(AB \perp ST\),則 \(ST\) 通過圓心。 |
|
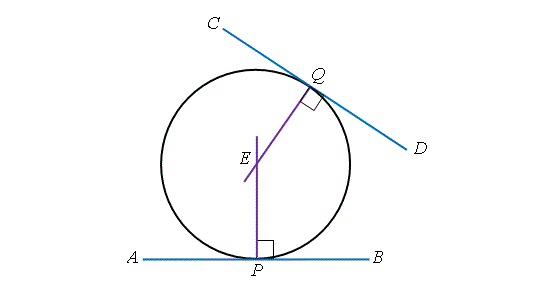
在圖右, \(AB \, 和 \, CD\) 分別是圓於 \(P\) 和 \(Q\) 點的切線。從這兩個切點,繪畫兩條直線垂直於切線,且設 \(E\) 為它們的交點。試判斷 \(E\) 是否這圓的圓心。