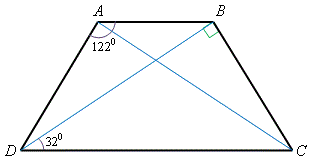
在右圖中, \(\angle BAD = 122^{\circ}\)、\(\angle BDC = 32^{\circ}\) 及 \(\angle CBD = 90^{\circ}\)。
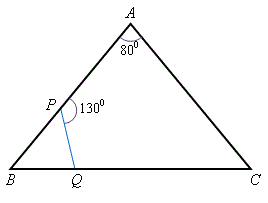
在右圖中, \(AB = AC\), \(\angle BAC = 80^{\circ}\) 及 \(\angle APQ = 130^{\circ}\)。
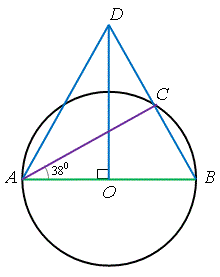
在右圖中, \(O\) 為圓心, \(AB\) 為直徑。弦 \(BC\) 延長至 \(D\) 使 \(DO \perp AB\)。若 \(\angle CAB = 38^{\circ}\),