若一些點位於在同一個圓形上,我們稱它們為共圓。
例如,在右圖中,\(A\)、\(B\)、\(D\,\) 及 \(\;E\) 為共圓點。
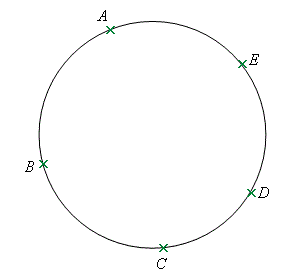
|
定理 20 任意三個非共線的點必定共圓,並且僅一個圓可以通過這三點。 |
在圖右, \(A\)、\(B\,\)和\(\,C\) 是三個共線的點。你能否構作一個圓來通過這三點?
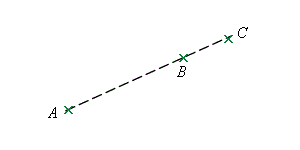
在上一課件,我們提及任意三個非共線的點必定共圓。但對於四個非共線的點,以上的說法是不成立。即是說,並非所有四個非共線的點必定共圓。
我們現在引用以下三個定理來判別四點是否為共圓點。
這是「定理 18」 的逆定理:
|
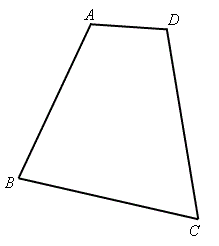
定理 22——對角互補 若四邊形 \(ABCD\) 的對角互補,則 \(A\)、\(B\)、\(C\,\)和\(\,D\) 四點共圓。 即,若\(\angle DAB + \angle BCD = 180^{\circ} \;\) 或 \(\angle ABC + \angle CDA = 180^{\circ} \; , \) 則\(A\)、\(B\)、\(C\;\)和\(\;D\) 四點共圓。 |
|
這是「定理 19」 的逆定理:
|
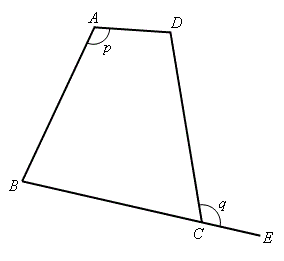
定理 23——外角 \(=\) 內對角 若四邊形 \(ABCD\) 的任每一個外角等於它的內對角,則 \(A\)、\(B\)、\(C\,\)和\(\,D\) 四點共圓。 即,若 \(q = p \),則 \(A\)、\(B\)、\(C\,\)和\(\,D\) 四點共圓。 |
|