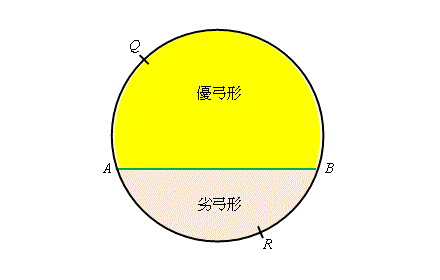
在右圖中， 由弦 \(AB\) 及劣孤 \(\overset{\frown}{AQB}\) 所形成的區域稱為 弓形 \(AQB\) (黃色部分)； 而由弦 \(AB\) 及優孤 \(\overset{\frown}{ARB}\) 所形成的區域稱為 弓形 \(ARB\) (粉紅色部分)。

1. 由於弓形 \(AQB\) 的面積 > 半個圓形的面積，弓形 \(AQB\) 稱為 優弓形。
2. 由於弓形 \(ARB\) 的面積 < 半個圓形的面積，弓形 \(ARB\) 稱為 劣弓形。

同弓形內的圓周角

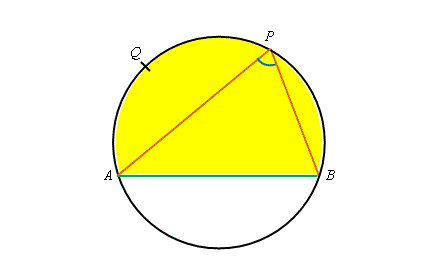
在右圖中， 劣孤 \(\overset{\frown}{AB}\) 所對的是圓周角 \(\angle APB\)。它位於著色的弓形 \(AQB\) 內。為直徑(即 \(AOB\) 是一條直線)，則 \(\overset{\frown}{AQB}\) 所對角 \(\angle APB\) 稱為 半圓上的圓周角。

現考慮以下兩個情景：

情景 \(1\)

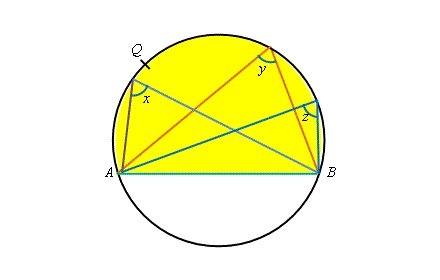
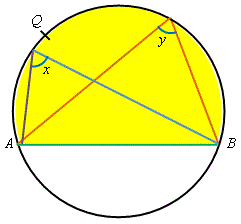
我們可於弓形 \(AQB\) 內，由同一段弧(劣弧) \(\overset{\frown}{AQB}\) 作出所對的圓周角，如 \(x、 \; y \; 及 \; z\) (見圖右)。這些角稱為 同弓形內的圓周角。

情景 \(2\)

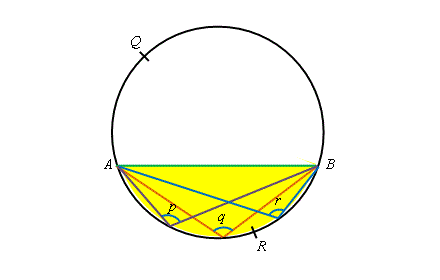
同理，我們可於同一段優弧 \(\overset{\frown}{ARB}\) 作出所對的圓周角，如 \(p、 \; q \; 及 \; r\) (見圖右)。這些角也稱為 同弓形內的圓周角。

在這一節中，我們將會以數學實驗來了解同弓形內的圓周角。

在右面的模擬模型，請移動 \(A\) 點或 \(B\) 點來改變劣弧的位置及大小。你也可移動數值滑桿來改變 \(P\) 點在圓周的位置。

根據右面的模擬模型中所得，請在以下列表的空格上填上適當的數字或答案。