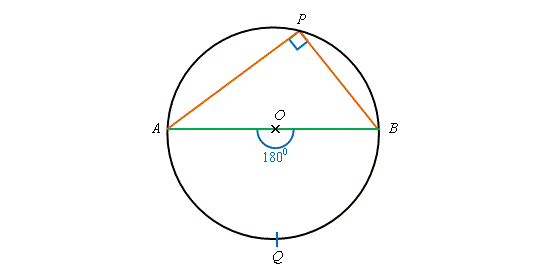
右圖中，設 \(O\) 為圓心及 \(AB\) 為直徑(即 \(AOB\) 是一條直線)，則 \(\overset{\frown}{AQB}\) 所對角 \(\angle APB\) 稱為 半圓上的圓周角。

根據定理 \(6\) '圓心角兩倍於圓周角'，我們可得：

\(\begin{align*} \angle APB &= \frac{1}{2} \angle AOB {\kern 40pt} \text{圓心角兩倍於圓周角} \\ &= \frac{1}{2} \times 180^\circ \\ &= 90^\circ \end{align*}\)

即，弧 \(\overset{\frown}{AQB}\) 所對的圓心角 \(\angle APB\) 是 \(180^\circ\)。

定理

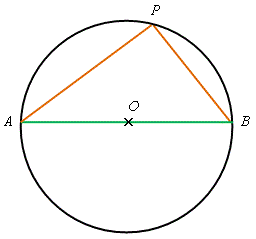
定理 \(7\) —— 半圓上的圓周角 半圓上的圓周角是一個直角。 即是說，若 \(AB\) 是一條直徑， 則 \(\angle APB = 90^\circ\)。

 

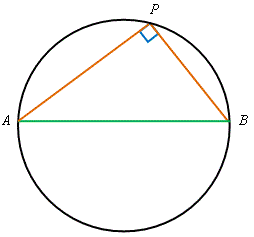
定理 \(8\) —— 半圓上的圓周角的逆定理 這是定理 \(7\) 的逆定理 若弦所對的圓周角是一個直角，則該弦是一條直徑。 即是說，若 \(\angle APB = 90^\circ\)， 則 \(AB\) 是一條直徑。