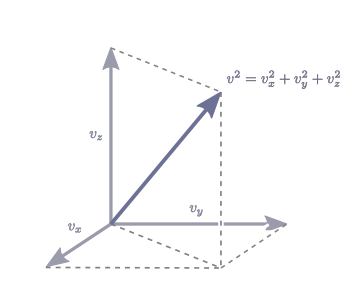
承接上一節的內容，若忽略重力的影響，那麼對於立方體容器中的氣體，\(x\), \(y\) 和 \(z\) 三個方向並無差別。所以在三個方向上容器內壁受到的氣壓是相同的，即 \[\begin{align} p &= \frac{N}{V} m\,\overline{v_x^2} = \frac{N}{V} m\,\overline{v_y^2} = \frac{N}{V} m\,\overline{v_z^2} \\\\ &=\frac{1}{3}\frac{N}{V} m\,\overline{v^2}\,,\end{align}\] 此處 \(v^2=v_x^2+v_y^2+v_z^2\) 為分子速度的平方，\(\overline{v^2}\) 即是分子速度平方的平均值。

由於一個分子的動能為 \(K=(1/2)\,m\,v^2\)，所以上式亦可表達為 \[p\,V=\frac{2}{3}N\,\overline{K} \,,\] 此處 \(\overline{K}\) 即是氣體分子的平均動能。比對普適氣體定律， \[p\,V=n\,R\,T\,\] 可以得到 \[\overline{K}=\frac{3\,R\,T}{2\,N_\textrm{A}}\,.\] 由此可見，氣體分子的平均動能正比於溫度。這便是氣體溫度在微觀上的意義。