在磁通量這概念的基礎上,科學家們了解到 法拉第定律 原來可寫成:
※※※ 感生電動勢的大小,與磁通量的變化率(或切割率)成正比 ※※※
若於時刻 \({{t}_{1}}\) 通過導體(或導體切割)的磁通量為 \({{\Phi }_{1}}\)、隨後於時刻 \({{t}_{2}}\) 通過的為 \({{\Phi }_{2}}\),則在時間 \(\Delta t\) = \({{t}_{2}}\) − \({{t}_{1}}\) 內,磁通量變化為 \(\Delta \Phi \) = \({{\Phi }_{2}}\) − \({{\Phi }_{1}}\),而磁通量的變化率就是 \({\Delta \Phi }/{\Delta t}\;\)。當磁通量與時間的單位分別是 \(\text{Wb}\) 和 \(\text{s}\),以單位伏特 (\(\text{V}\)) 為感生電動勢(設符號為 \(\varepsilon \))的話,法拉第電磁感應定律的表達式為:
\(\displaystyle{\varepsilon =-\frac{\Delta \Phi }{\Delta t}}\)
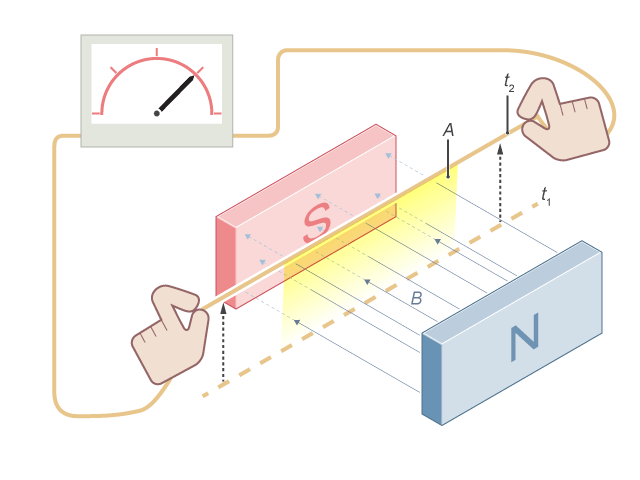
由於 \(\Phi =B\ A\cos \theta \),即只需 \(B\)、\(A\)、\(\theta \) 中其中一項出現變化,便有感生電動勢。留意上式中的負號乃反映了 \(\varepsilon \) 的 "方向",表明感生電動勢的正負總是與磁通量變化率的正負相反,這其實是概括了楞次定律對感生電流方向的規律;如將磁鐵插入線圈時(),\({{t}_{2}}\) 時會較 \({{t}_{1}}\) 有更多磁場線穿越線圈截面,而:
當僅需關注感生電動勢的大小時,可以省去表達式中的負號。
對於一個很密的 \(N\) 匝線圈(),由於穿過每個線圈的磁通量相同,當磁通量起變化時,每個線圈都產生相同的 \(\varepsilon \),由這些線圈造成的 \(\varepsilon \) 便猶如電池串聯,所以 \(N\) 匝線圈的法拉第定律是:
\(\displaystyle{\varepsilon =-N\frac{\Delta \Phi }{\Delta t}=-\frac{\Delta \left( N\Phi \right)}{\Delta t}}\)
記得 \(N\Phi \) 就是磁通匝鏈數。
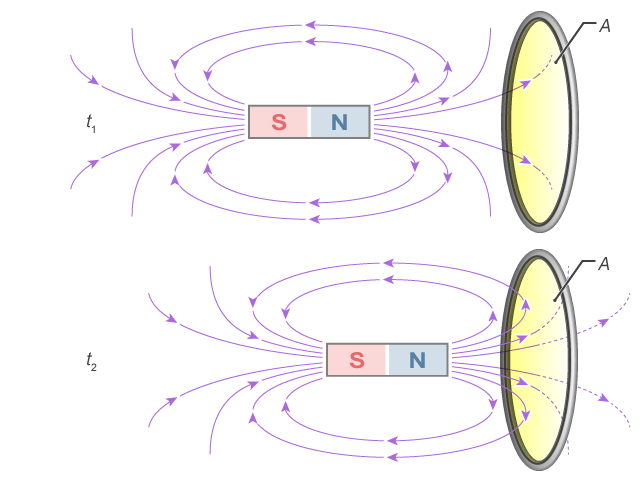
在的電磁感應實驗,磁通量的改變乃基於磁鐵與線圈間有相對運動時,穿過線圈截面的磁場線的數目起了變化(增多了)。那麼在類似的實驗,導線因切過磁場線會造成感生電動勢,磁通量的變化是怎樣的?對於這種情況:
※※※ 感生電動勢 \(=\) 單位時間內所掃過的磁通量 ※※※
若於時間 \(\Delta t\) = \({{t}_{2}}\) − \({{t}_{1}}\) 內,導線如所示般被拉向上、切割勻強磁場 \(B\);導線於磁場範圍裡所掃過的面積是 \(A\),則磁通量變化就是 \(BA\)。
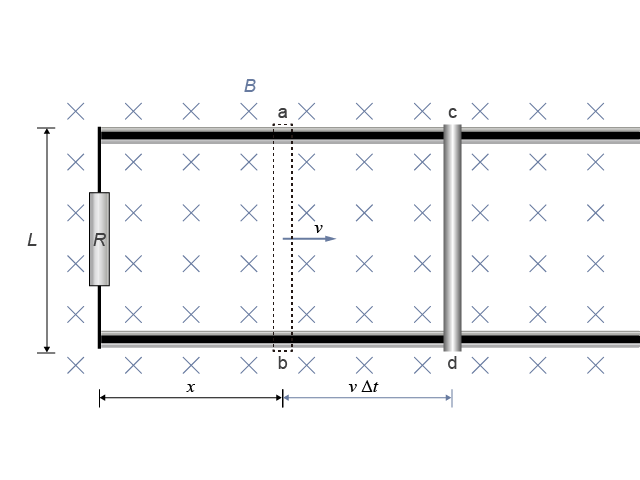
例子是一個類似的系統,導體棒在勻強磁場 \(B\) 中(方向為指入畫面)被推向右,儘管過程中磁場的強弱不變,但磁場線會被右移的導體棒切過。設兩相距 \(L\) 的平行金屬軌連接電阻器 \(R\),導體棒放在軌間便形成閉路;現從位置 \(\text{ab}\) 以勻速 \(v\) 右移至 \(\text{cd}\)、耗時 \(\Delta t\),而棒掃過的面積等於 \(L\left( v\Delta t \right)\)。由於 \(B\) 總是垂直於棒掃過的面積,換言之,感生電動勢與感生電流 (\(i\)) 的大小分別就是:
\(\displaystyle{\varepsilon =\frac{\Delta \Phi }{\Delta t}=\frac{BL\left( v\Delta t \right)}{\Delta t}=BLv}\)
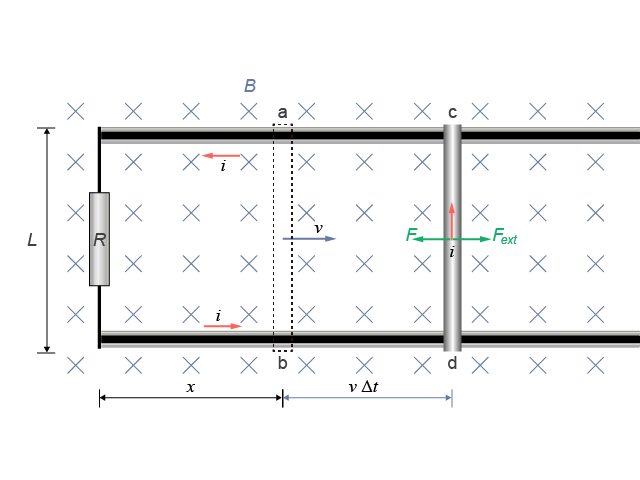
由於導體棒右移,根據弗林明右手定則,可將右手姆指(代表運動方向)和食指(代表磁場方向)分別指向右和指入畫面,這時候中指(代表感生電流方向)會指向上,表示導體棒上的感生電流會從 \(\text{d}\) 流向 \(\text{c}\),即感生電流沿所示的閉路乃呈逆時針方向。
由此我們亦可知 \(R\) 所消耗的電功率 \(P={{i}^{2}}R={{{B}^{2}}{{L}^{2}}{{v}^{2}}}/{R}\;\)。
隨着電流 \(i\) 流過導體棒,處於磁場 \(B\) 下的導體棒便會受到一大小為 \(BiL\sin \alpha \) 的磁力 \(F\),方向由弗林明左手定則給出;\(\alpha \) 是電流方向與 \(B\) 之間的夾角,故:
\(\displaystyle{F=B\ iL\sin 90{}^\circ =\frac{{{B}^{2}}{{L}^{2}}v}{R}}\) (方向指向左)
這揭示了為要令中的導體棒維持勻速往右移,必須對其施以一外力 \({{F}_{ext}}\)(見),這個外力與 \(F\) 的大小相同、而方向相反。