根據電磁感應實驗的結果,導體切割磁場線和外磁場變化的率,是影響感生電動勢的因素。那麼,這些因素與感生電動勢的關係是怎樣的?能以定量方法來描述法拉第定律嗎?事實上,法拉第於解釋電磁感應現象時,引入了所謂磁通量 (magnetic flux) 的概念。之後我們便會了解到,原來造成感生電動勢的條件,就是穿越導體回路的磁通量要發生變化。
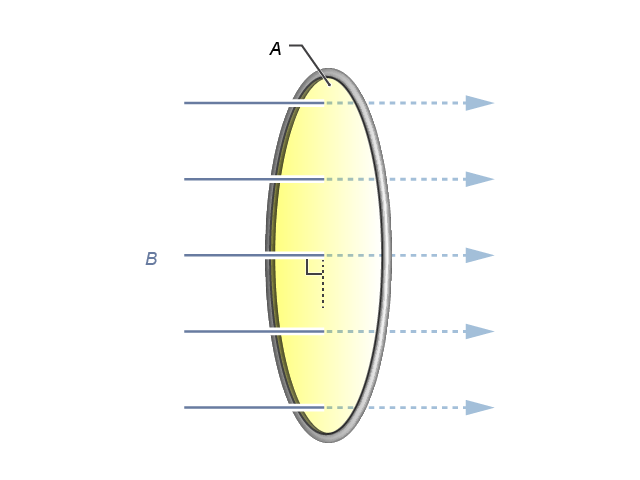
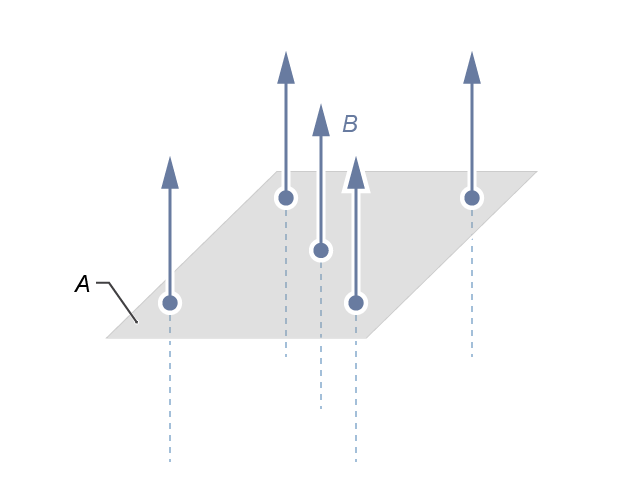
當討論涉及穿過某一面積的磁場及其變化時,往往會用到磁通量。如所示,設在一磁場大小為 \(B\) 的勻強磁場中,有一垂直於磁場方向、面積為 \(A\) 的平面;穿過這個面的磁通量就定義為 \(B\) 和 \(A\) 的乘積,以符號 \(\Phi \) 表示。即:
\(\Phi =BA\)
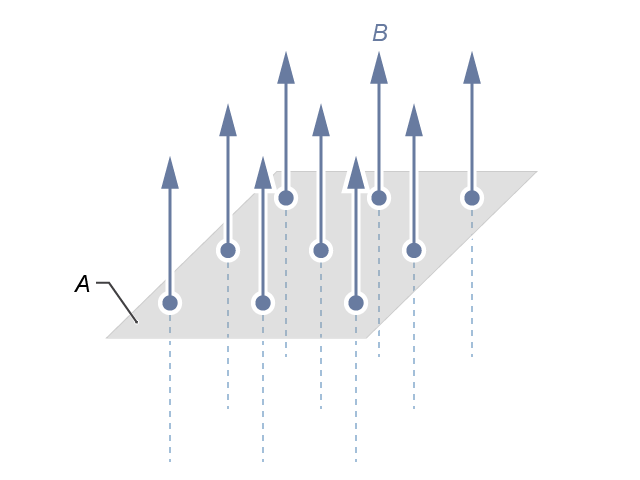
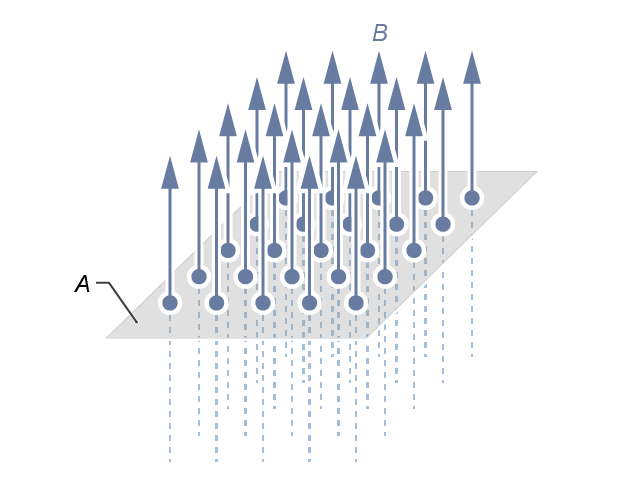
磁通量是一個標量,其國際單位制單位為 韋伯 (weber),簡寫為 \(\text{Wb}\);\(1\ \text{Wb}\) 亦相等於 \(1\ \text{T}\ {{\text{m}}^{2}}\)。記得 \(B\) 這個物理量描述了磁場中 某點 上的強弱和方向,當 \(B\) 愈大,表示磁場愈強,會用較密的磁場線表示(比較至)。基於這個思路,磁通量可看成為穿越一個面的磁場線的多少,它指出了磁場中某個面上的總體情況。換言之,如果、和裡,磁場通過的那塊面有相同面積,而三種情況中的磁通量分別為 \({{\Phi }_{1}}\)、\({{\Phi }_{2}}\) 和 \({{\Phi }_{3}}\),可知:
若您自覺仍未能充分掌握磁通量的意義,試將它類比於光通過牆洞的情況,可視為「光通量」,其大小取決於光的強弱(磁通量中的磁場的類比)以及牆洞的有效面積(磁通量中的討論面積的類比)。
由 \(\Phi =BA\) 這關係可知,\(B\) 等於穿過垂直於磁場方向的單位面積的磁通量:
\(\displaystyle{B=\frac{\Phi }{A}}\)
故此,磁場強度 \(B\) 這個物理量其實有另一個名字,稱為 磁通量密度 (magnetic flux density),而 \(B\) 亦可以用韋伯每平方米作為單位,簡寫為 \(\text{Wb }{{\text{m}}^{-2}}\)。
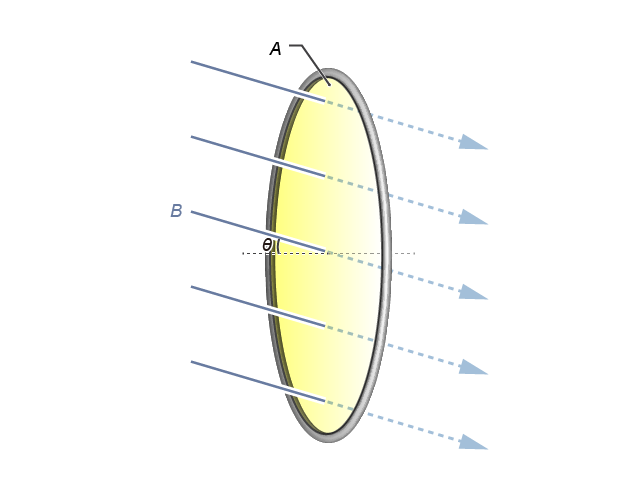
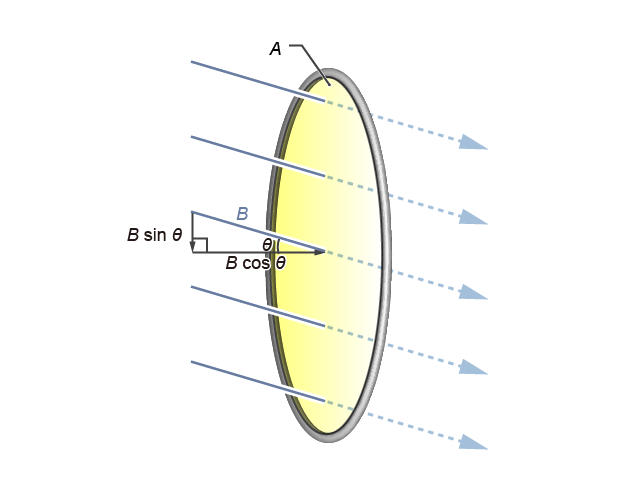
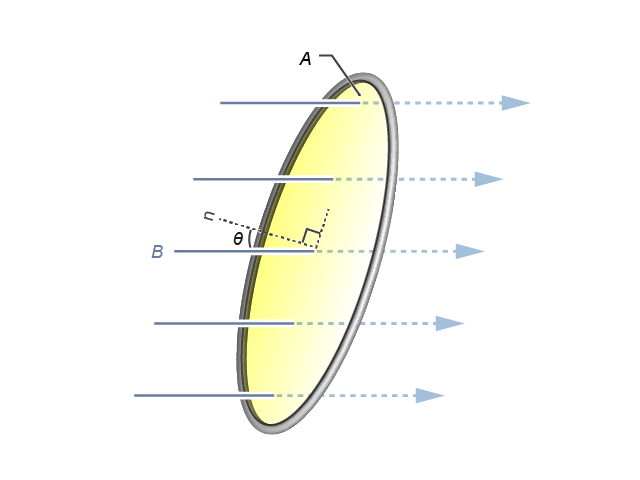
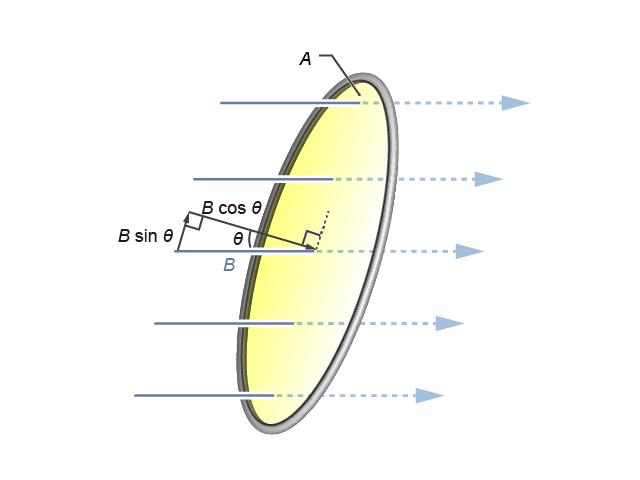
在電磁感應的問題上,磁通量中所指的面積 \(A\),往往就是線圈的橫截面積,如就是一組勻強磁場 (\(B\)) 垂直穿過一圓形線圈的示意圖。然而,磁場方向與我們要關注的平面乃不一定互相垂直的,例如像所示般,磁場方向便與平面法線成一夾角 \(\theta \)。對於這情況,我們可以對 \(B\) 作矢量分解(見),而只有垂直於線圈截面的分量 \(B\cos \theta \) 才會影響磁通量。因此,磁通量的表達式可一般化地寫成 \(\Phi =\left( B\cos \theta \right)A\),或:
磁通量 \(\Phi =B\ A\cos \theta \)
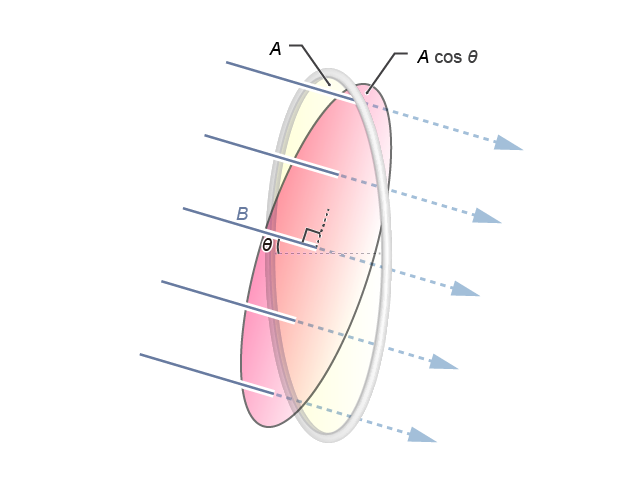
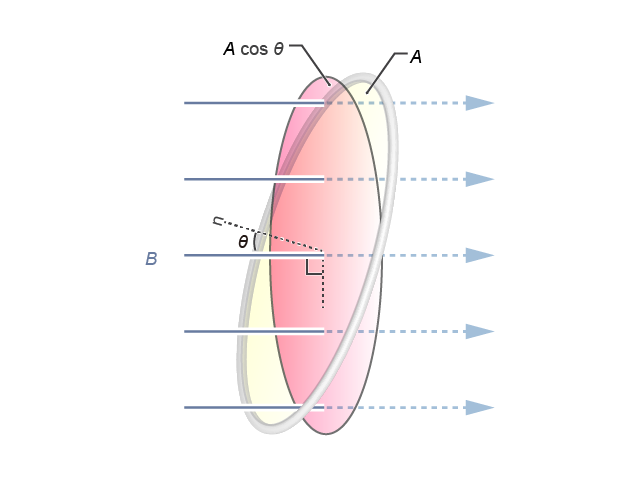
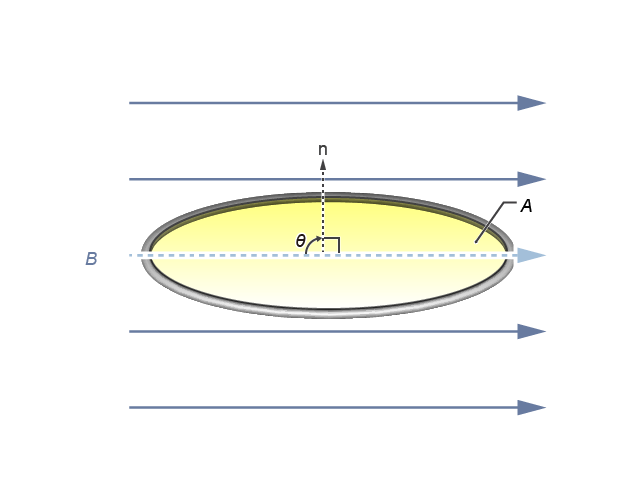
分析這類問題時,除對 \(B\) 作矢量分解外,我們也可以如般,考慮線圈平面在垂直於磁場方向的投影,該投影的面積就是 \(A\cos \theta \)。即磁通量為 \(\Phi =B\left( A\cos \theta \right)\),結果與上方算式相同。同理,如果磁場方向水平、而線圈平面傾斜();平面法線與磁場方向成夾角 \(\theta \),本質上便與完全相同,磁通量的表達式仍為 \(\Phi =B\ A\cos \theta \)。
您或從 \(\Phi \) 的表達式已察覺,由於 \(0\le \left| \cos \theta \right|\le 1\),對於給定大小的 \(B\) 和 \(A\):
若上方討論的 \(\Phi \) 是通過截面積為 \(A\) 的 \(N\) 匝線圈裡的其中一匝的磁通量,則通過整個線圈的總磁通量會是 \(N\Phi \),稱為 磁通匝鏈數 (magnetic flux leakage):
磁通匝鏈數 = \(N\Phi \)