探察線圈 (search coil) 是一種應用了電磁感應原理的儀器，常用於量度會變化的磁場大小。

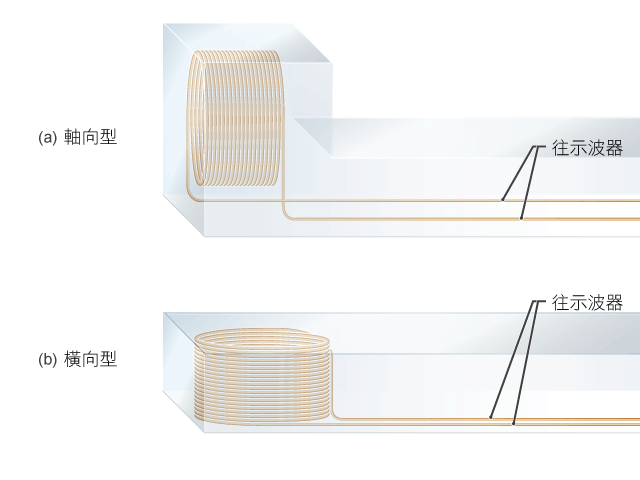
所示為學校實驗室中常見的探察線圈。一端是一個匝數很多、呈扁平的細小線圈，通常具有 2000 至 5000 匝，平均截面積為 \({{10}^{-4}}\ {{\text{m}}^{2}}\)；設於另一端的電線插座乃供接駁往示波器以顯示訊號。把探察線圈放置在要量度的磁場裡時，若線圈截面與磁場平行，是不會形成感生電動勢的；故此在量度時，會視乎情況使用軸向型 (axial) 或橫向型 (lateral) 的探察線圈，分別為其線圈乃垂直還是平行於手柄（見、）。

量度時，若將截面積為 \(A\)、含 \(N\) 匝的探察線圈放在變化中的磁場，會在線圈兩端感應出一個電動勢，其大小為：

\(\displaystyle{\varepsilon =-N\frac{\Delta \Phi }{\Delta t}=-NA\frac{\Delta B}{\Delta t}}\)

由於 \(B\) 隨時間變化，\({\Delta B}/{\Delta t}\;\) 即是某時刻的 \(B\) 隨時間變化的快慢程度，而 \({\Delta B}/{\Delta t}\;\) 往往並非一個常數。因 \(B\) 的變化率往往不定，故 \(\varepsilon \) 亦變化不定，我們可以將探察線圈接駁到示波器，以便於觀察和記錄 \(\varepsilon \)。

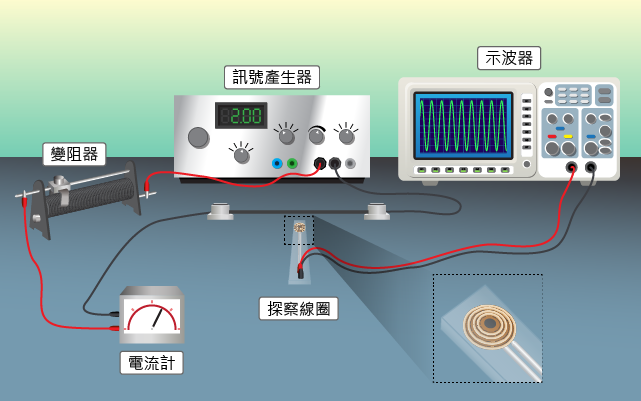
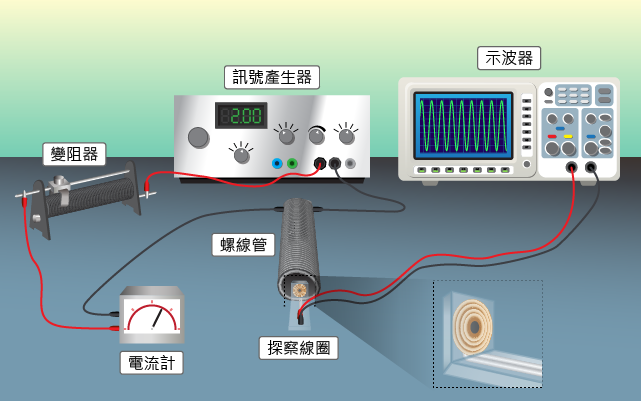
例如要量度一根載電長直導線外的磁場，又或者螺線管內的磁場時，和分別顯示兩情況下於水平桌上的設置。由於長直導線外的磁場線是以導線為中心的同心圓，而螺線管內的磁場線則是從一端指往另一端的直線，故此：

• - : 探察線圈
• - : 量度變化磁場的設置

• : 外觀
• : 放大圖
• : 結構圖

安裝在細長的絕緣手柄上的探察線圈，以便於伸往不同位置去量度磁場。(a) 軸向型；(b) 橫向型

(a) 軸向型的探察線圈，線圈截面垂直於手柄；(b) 橫向型的探察線圈，線圈截面平行於手柄

(a) 軸向型的探察線圈，線圈截面垂直於手柄；(b) 橫向型的探察線圈，線圈截面平行於手柄

• : 長直導線
• : 螺線管

量度一根載電流長直導線外的磁場

量度一個載電螺線管內部的磁場

上方的 \(\varepsilon \) 表達式顯示，量度結果會取決於 \(B\) 的變化，而 \(B\) 如何隨時間變化乃視乎其產生方式；若這個要量度的磁場為正弦變化（見(a)），可表示成：

\(B\) = \({{B}_{0}}\cos 2\pi ft\)     

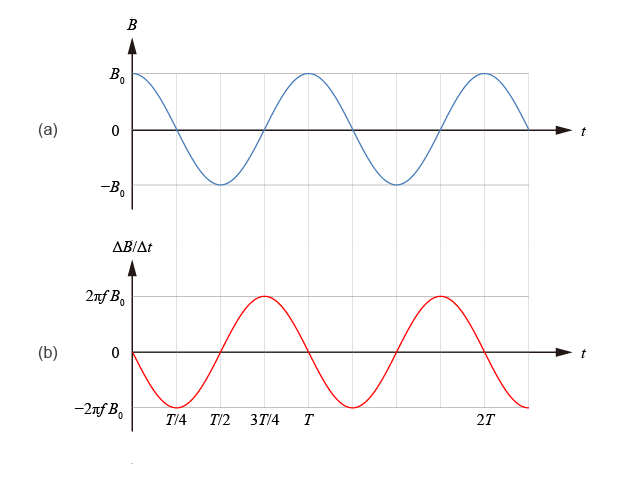
\({{B}_{0}}\) 與 \(f\) 分別為波的振幅和頻率。(a) 清楚顯示 \(B\) 隨時間變化不定，而這個關係圖線亦不是一條直線，即 \(B\)-\(t\) 線圖中的斜率不是一個常數。事實上，\({\Delta B}/{\Delta t}\;\) 可被視為 \(B\)-\(t\) 線圖上的瞬時變化的斜率。仔細檢視(a) 可察覺：

• 當 \(t=0\)，這刻的斜率 = 0；
• 當 \(t=\left( n+{1}/{4}\; \right)T\)，這刻的斜率為負、量值最大；
• 當 \(t=\left( n+{1}/{2}\; \right)T\)，這刻的斜率 = 0；
• 當 \(t=\left( n+{3}/{4}\; \right)T\)，這刻的斜率為正、量值最大；
• 當 \(t=\left( n+1 \right)T\)，這刻的斜率 = 0。

其中 \(n\) 是零或正整數 (0, 1, 2, 3, ‧‧‧‧‧‧)、\(T\) 代表週期。我們亦可進一步檢視以上各相鄰時刻之間的斜率，有關結果可參考。事實上，更深入分析斜率於各時距的變化可知，這個斜率隨時間的變化亦為正弦關係，為 \({\Delta B}/{\Delta t}\;\)= \(-2\pi f{{B}_{0}}\sin 2\pi ft\)，有關圖線會如(b) 所示。換言之，對於正弦變化的 \(B\)，\({\Delta B}/{\Delta t}\;\) 仍是正弦變化，但與 \(B\) 有 \(90{}^\circ \) 相位差。由此可寫出：\(\varepsilon \) = \({{\varepsilon }_{0}}\sin 2\pi ft\)，而：

\({{\varepsilon }_{0}}=2\pi fNA{{B}_{0}}\)

在諸如和的設置中，由於 \({{\varepsilon }_{0}}\) 和 \(f\) 可以從示波器顯示的圖像中讀出，而 \(N\) 和 \(A\) 是儀器的參數，藉上式便可找出要量度的磁場的振幅 \({{B}_{0}}\)。