接下來,我們再進行實驗,觀察駐波如何形成。將軟彈簧放在地上,把彈簧的一端連接堅固的支撐物,使其成為固定末端。拉直軟彈簧,然後不斷抖動彈簧的另一端,並逐漸提高抖動頻率,同時留意波的形狀。便播放了這實驗的演示;細心觀看並留意影片最後部分(提高抖動頻率後),可知:
駐波常見於在樂器中的管、弦、膜等的振動,如結他弦線上的振動,便是由駐波所形成的振動:

從觀察所得,在特定的抖動頻率下,彈簧上會形成一個或多個不停振動的波圈(另見)。這種波既不前進也不後退,稱為駐波 (stationary wave / standing wave)。這情況中,彈簧上的駐波有多達 3 個波圈。
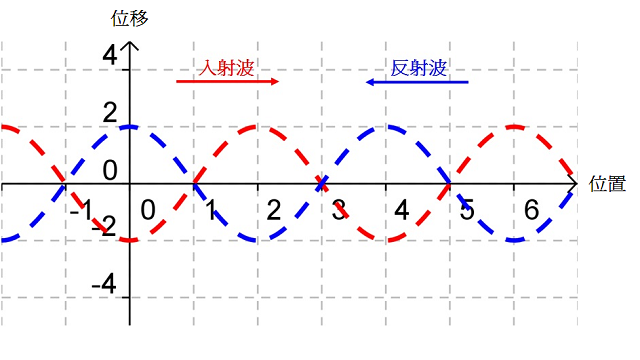
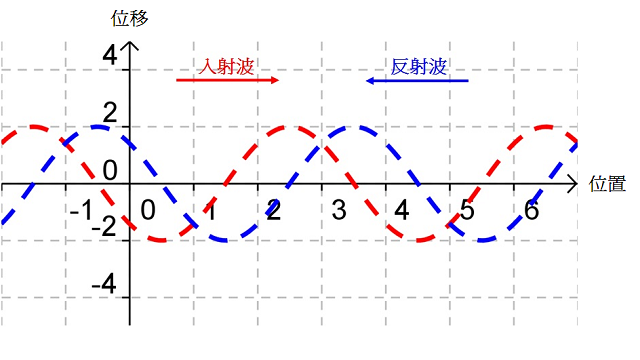
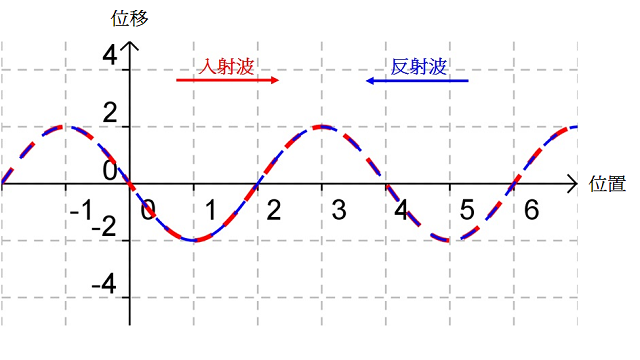
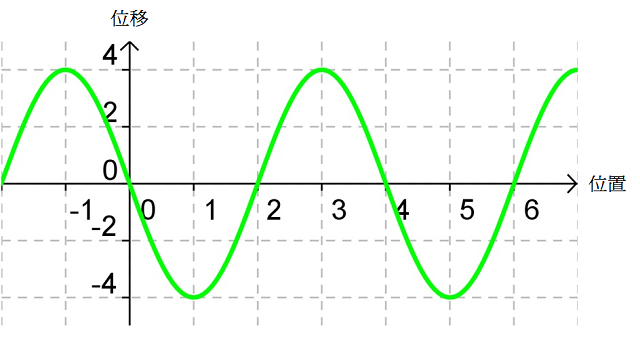
為甚麼駐波會出現呢?別忘記,入射波和反射波同時出現在彈簧上,它們會疊加起來,形成新的波形(見);在特定的頻率下,入射波和反射波會發生干涉,形成一個或多個不停振動的波圈,波圈既不前進也不後退。總括而言:
駐波是由兩個振幅、頻率、速率都相同的行波,以互相相反的方向傳播時疊加而成。
留意剛才雖一直以固定端反射形成的駐波來說明,若在一根彈簧的兩端各有一個波源,造出兩個振幅、頻率、速率都相同而朝另一端傳播的行波,它們相遇時亦能形成駐波。

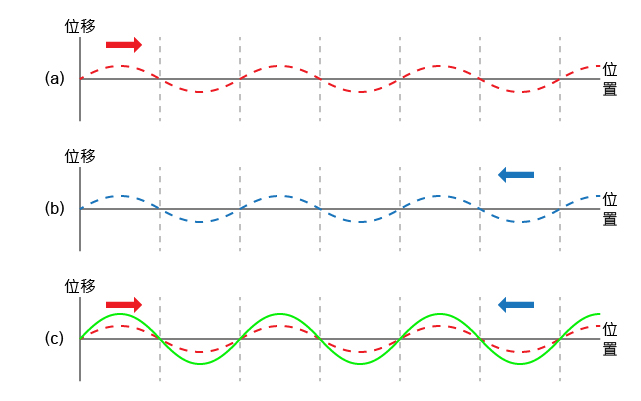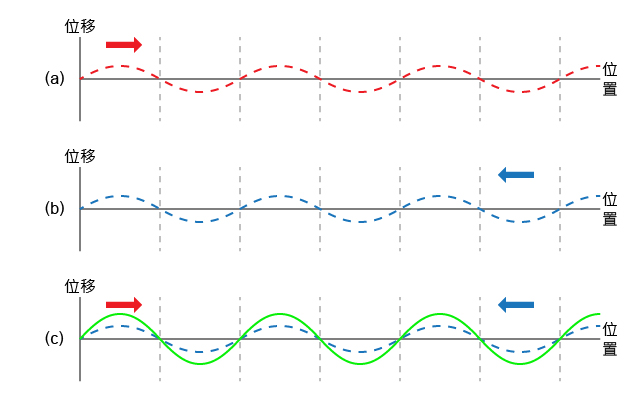
雖然駐波的波圈既不前進也不後退,其形狀會隨時間改變嗎?
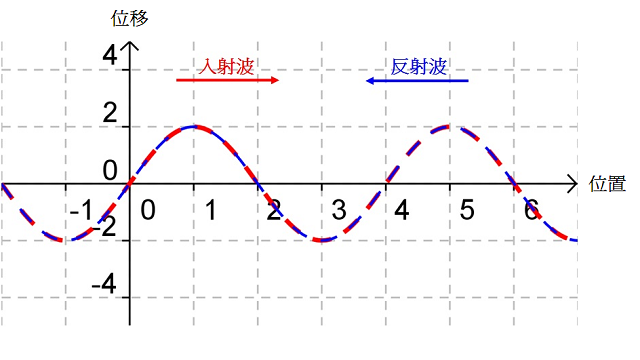
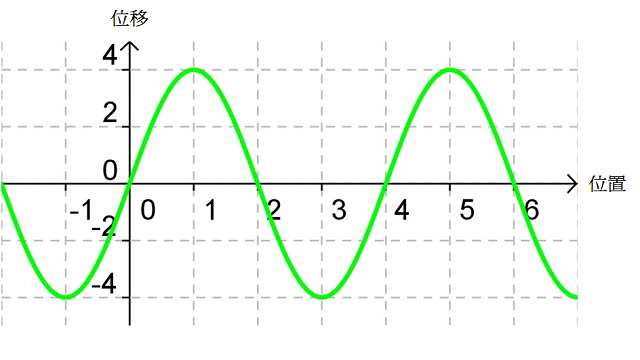
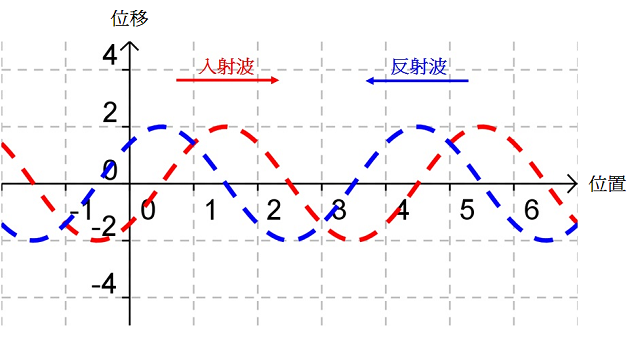
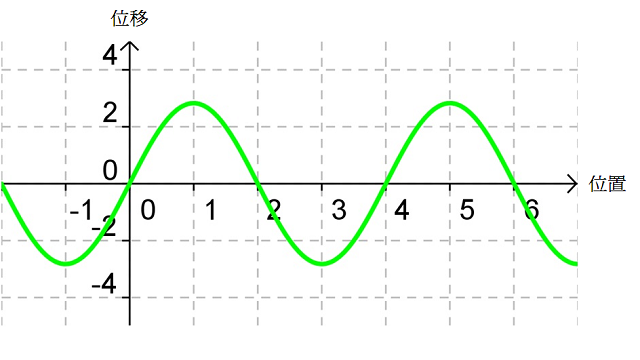
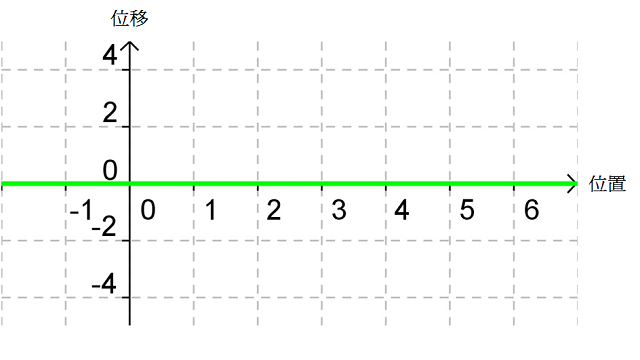
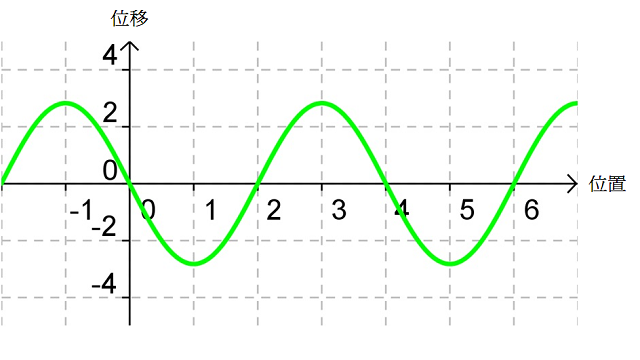
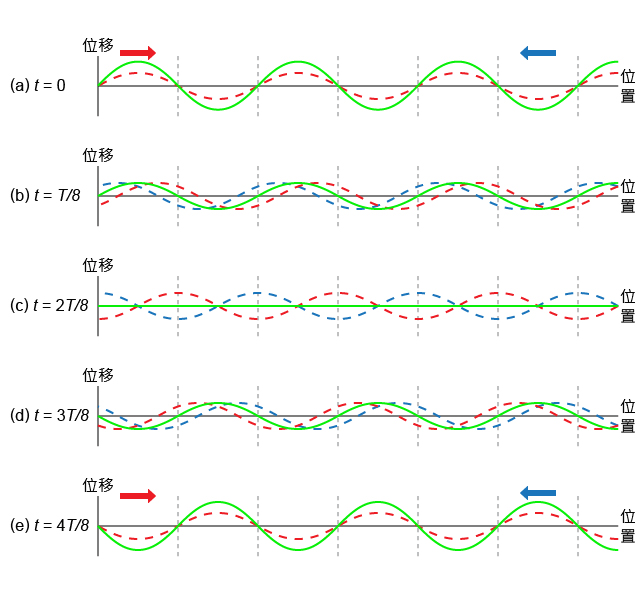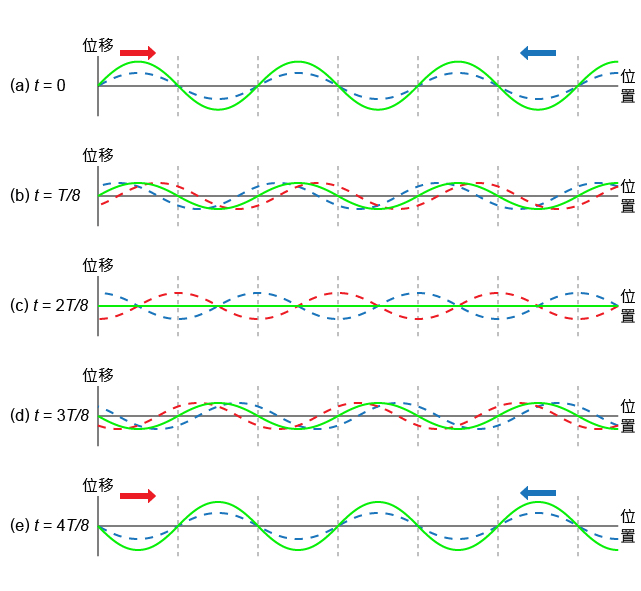
考慮中的入射波(紅線)和反射波(藍線),疊加後形成的駐波(綠線)便如所示(亦相當於(c) 所示狀態)。設該時刻為 \(t=0\)、波的週期等於 \(T\),、、 和 便是隨後每經過時距 \({T}/{8}\;\) 後的駐波波形;、、 和 則是對應時刻的入射波和反射波。比較、、、 和 可知,駐波的波圈不行進、波形卻會隨時間不斷變化。
事實上,駐波的波形是會週而復始地以固定方式重複變化的。便把剛才從 \(t\) = \(0\) 至 \({T}/{2}\;\) 的波的變化,顯示在同一幅圖上以供比較。留意 \(t\) = \(0\) 的合成波與 \(t\) = \({T}/{2}\;\) 的上下對稱;\(t\) = \({T}/{8}\;\) 的合成波與 \(t\) = \({3T}/{8}\;\) 的上下對稱。若把 \(t\) = \({T}/{2}\;\) 隨後再過每 \({T}/{8}\;\) 後的兩個波形繪出來,會發現 \(t\) = \({5T}/{8}\;\) 的合成波會與 \(t\) = \({3T}/{8}\;\) 的相同;而 \(t\) = \({3T}/{4}\;\) 的合成波則與 \(t\) = \({T}/{4}\;\) 的相同。您亦可藉以下模擬程式設定振幅與波長相等的兩正弦波相遇,觀看合成波的波形變化:
本質上,駐波只是干涉現象的一個特例而已。您能判斷在時間 \(t\) = \(0\)、\({T}/{4}\;\) 和 \({T}/{2}\;\) 時,入射波和反射波在發生相長還是相消干涉嗎?