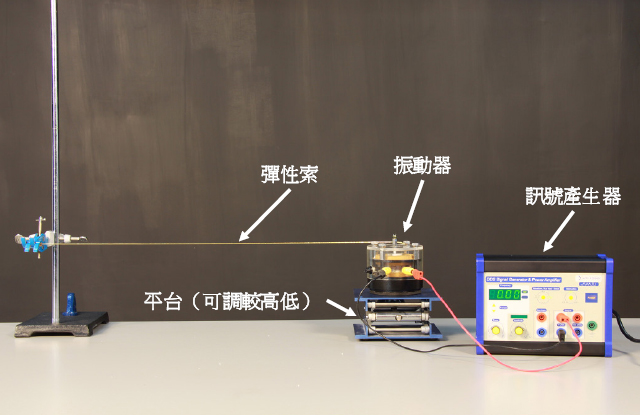
除了用手抖動彈簧能造成駐波外，振動器亦能產生駐波。首先將彈性索的一端綁緊到振動器上，再稍為拉長另一端並用鉗子夾住，令彈性索有一定張力。調較平台高底，令彈性索達至水平，然後把振動器連接到訊號產生器。便顯示了這組實驗裝置。

要在彈性索上形成駐波，只需啟動訊號產生器後，慢慢調高輸出頻率至某個數值，便能令彈性索上形成一個波圈的駐波，如所示。

若在的基礎下，不斷調高輸出頻率，情況會如般：

接着，假使我們再繼續不斷調高輸出頻率（見）：

事實上，若再進一步調高輸出頻率，將能產生更多波圈。

在或，當輸出頻率正在調高時，您有留意到波圈會消失一會後才重新出現嗎？這仿佛表示，駐波只能在特定頻率下產生？頻率需滿足甚麼條件嗎？接下來我們將分析這個問題。

當繩弦上只有一個波源，行波在繩弦末端反射後，形成入射波和反射波疊加，便必定會形成駐波嗎？我們可以根據的駐波實驗的設置，分析形成駐波的條件（如有）。

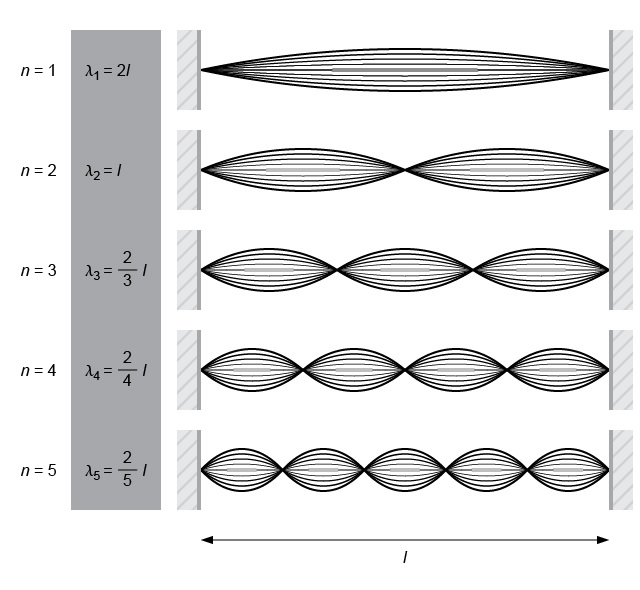
若繩弦的兩端都是固定端時，當我們抖動繩弦使之振動，產生的波經兩固定端反射，相互干涉，疊加後所形成的駐波將如所示。對於固定端，由於反射波有 \(180{}^\circ \) 相變，駐波（即合成波）在固定端位置的位移必定等於零。設正弦波的波長為 \(\lambda \)、頻率為 \(f\)，則繩弦的長度 \(l\) 必定是 1/2 個波長的整數倍，即：

\(\displaystyle{l=n\ \frac{{{\lambda }_{n}}}{2}}\)

其中 \(n\) 是大於零的整數 (1, 2, 3, ‧‧‧‧‧‧)；\({{\lambda }_{n}}\) 代表不同波長的情況。若繩弦上行波的行進速率等於 \(v\)，則繩弦的振動頻率（也是駐波的頻率）等於：

\(\displaystyle{{{f}_{n}}=\frac{v}{{{\lambda }_{n}}}=\frac{n\ v}{2\ l}}\)

換言之，可產生駐波的頻率並非任意的。在上式，\({{f}_{1}}\) 即是只有 1 個波圈時的振動頻率，\({{f}_{2}}\) 是有 2 個波圈時的振動頻率，如此類推。再者，由於 \({{f}_{2}}\) = 2 \({{f}_{1}}\)，\({{f}_{3}}\) = 3 \({{f}_{1}}\)，‧‧‧，所以 \({{f}_{n}}\) 亦可寫成：