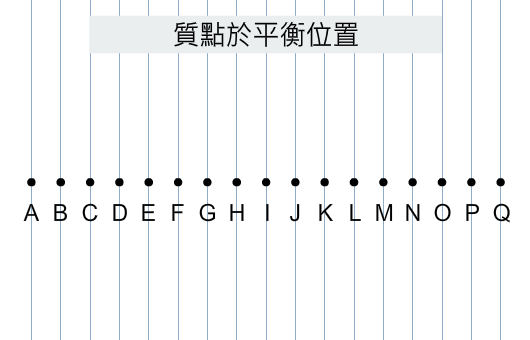
探究波的運動時,先要知道何謂平衡位置 (equilibrium position)。在軟彈簧上,每個螺旋圈的平衡位置,就是在沒有波傳播時,它們所處的位置。下圖就顯示了一根拉長的軟彈簧上每個螺旋圈的平衡位置,可見:

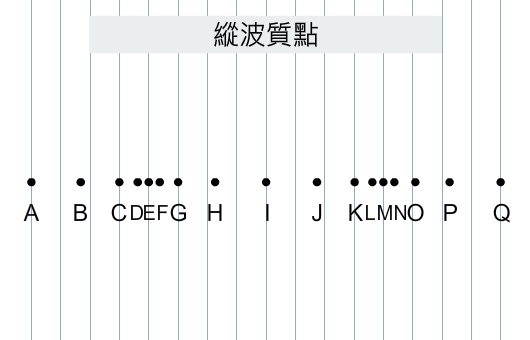
探究波動時,可用一串質點來表示波:是未有波傳播的情況,所有質點位於其平衡位置;和分別是某一刻的橫波和縱波,留意每個質點跟其平衡位置時相距有多遠!在下一課,我們將會討論質點運動,當中涉及質點位移這概念,其實就是指質點相對於其平衡位置的距離和方向。
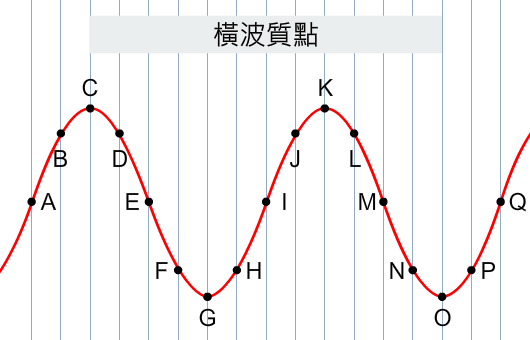
同一類型的波,都有各式各樣的波形。如橫波,有些波峰會高些、有些會矮些;有些波峰間相距遠些、有些相距近些。要描述和分辨波形,應先掌握一些描述波的變量,包括振幅 (amplitude)、波長 (wavelength)、波速 (wave speed)、週期 (period) 和頻率 (frequency):
波的振幅、又稱波幅,是質點相對於平衡位置的最大位移。振幅通常以符號 \(A\) 來表示、其量度單位是 \(\text{m}\)(米)。
找出波幅最直接的方法,就是量度質點的最大位移。在及中,就看到了波中質點的最大位移,即是波幅 \(A\) 了。
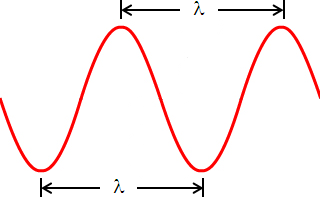
如何從波形中找橫波振幅?在橫波上,於波峰的最高點及於波谷的最低點、質點的位移是最大的。故此,波峰最高點和平衡位置之間的距離,及波谷最低點和平衡位置之間的距離,都等於波幅,如下方的正弦波形所示:
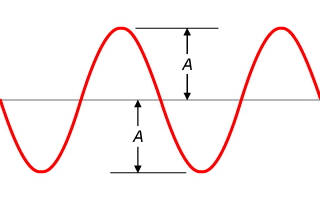
至於縱波,就不能直接從波形中找出波幅了。
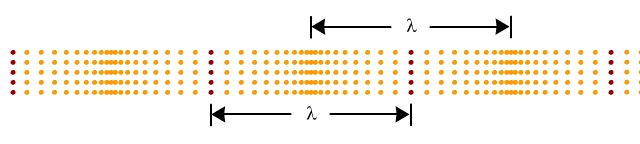
波長是波中任何兩個既振動步調一致,又最接近的質點之間的距離。波長通常以符號 \(\lambda \) 表示,其量度單位是 \(\text{m}\)(米)。(\(\lambda \) 是希臘字母,英文叫作 lambda)
及演示了橫波及縱波的質點運動。若兩質點相距一個波長,它們的步調便一致,換言之它們會在同一時間到達最大位移及平衡位置。
要簡便地從波形中找出波長,可考慮使用以下兩項特性來量度:
傳播中的波,波形乃移動著的。波形移動的速率,就是波速,又即是單位時間內波形所傳播的距離。
由於波速是波的傳播速率,而波會傳遞能量,所以:
波速 \(=\) 波動能量傳送的速率
波速通常以符號 \(v\) 表示,量度單位是 \(\text{m }{{\text{s}}^{-1}}\)。如果能記錄不同時間的波形,就能找出波速。
細心留意和裡的質點運動,會發現:
雖然波在傳播時其波形會移動,但介質中的質點是不會隨波形前進的。這些質點只會在平衡位置附近振動著、時快時慢。
換言之:
波速 \(\ne \) 質點運動速率
波傳播之際,質點完成一次完整振動的時間,稱為週期。週期通常以符號 \(T\) 表示,其量度單位是秒 (\(\text{s}\))。
【概念 1】 何謂一次完整的振動?
質點做完一次完整振動,可簡述為振動了一次。以橫波來說(見),當一個質點從某個位置開始,上升到最高點(或下降到最低點),然後下降到最低點(或上升到最高點),再返回原本位置,那麼質點就做完一次完整振動。和分別演示了橫波和縱波質點在一週期內的運動。
【概念 2】 在一週期內,波形有何改變?
例如在橫波的情況,從的演示可見:
綜合以上兩項可知,於波傳播期間:
每當質點振動了一次,便過了一週期,波形移動了一波長的距離。
波的頻率是質點每秒內的振動次數。頻率通常會用符號 \(f\) 來表示,單位是赫茲 (\(\text{Hz}\)),其中 \(\text{Hz}\) 為英文 Hertz 的簡寫。以赫茲表示頻率,是為了紀念德國物理學家赫茲 (Heinrich Rudolf Hertz) 證實電磁波存在的事蹟。

如果波中的質點在一秒內振動 1 次,波的頻率是 1 \(\text{Hz}\);如果波中的質點在一秒內振動 2 次,波的頻率是 2 \(\text{Hz}\);如此類推。以下活動比較了不同頻率高低的質點的振動:
您有否從以上體會到,當頻率愈高,質點的振動會愈快?和分別演示了波速相同、但頻率不同的橫波和縱波。