從質點振動的頻率 (\(f\)) 與週期 (\(T\)) 的定義,應不難發現,它們之間有這關係:
\(\displaystyle{f=\frac{1}{T}}\)
運用這關係,便可從週期計算出頻率,或從頻率計算出週期。注意,從以上公式中,可推導出頻率單位 \(\text{Hz}\) 其實等同於 \({{\text{s}}^{-1}}\)。例如要分別找出振動頻率為 10 \(\text{Hz}\) 的質點的週期,以及週期為 5 \(\text{s}\) 的另一質點的頻率,計算就是:
\(T\) = 1 / (10 \(\text{Hz}\)) = 1 / (10 \({{\text{s}}^{-1}}\)) = 0.1 \(\text{s}\) \(f\) = 1 / (5 \(\text{s}\)) = (1/5) \({{\text{s}}^{-1}}\) = 0.2 \(\text{Hz}\)
在波傳播之際,原來質點的頻率,也跟波長和波速之間有一個簡單數學關係:
\(\displaystyle{\lambda=\frac{v}{f}}\)
其中 \(\lambda \) 為波長、\(v\) 為波速、\(f\) 為頻率。這方程有時會稱為波動方程,運算例子可參考和。留意波動方程適用於所有類別的連續波。
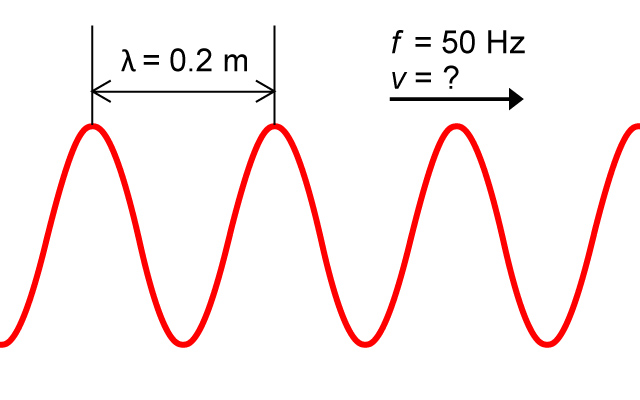
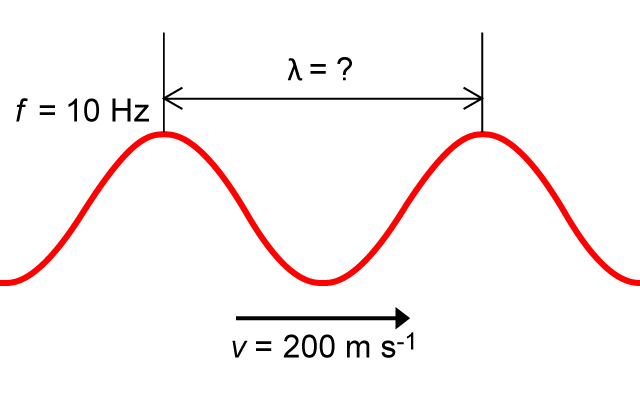
行波可由振幅 \(A\)、頻率 \(f\)、波長 \(\lambda \)、波速 \(v\) 等波的性質描述。那麼,有何因素影響波速?我們可再於軟彈簧上造出脈衝(),變動這些量進行探究:
探究結果顯示,波速與軟彈簧性質有關。事實上,波在軟彈簧上傳播時,振幅和頻率不會影響波速。而彈簧上的張力愈大(),波速愈大。原來在軟彈簧上(或張緊絃線上),行波的波速是由以下關係決定:
\(\displaystyle{v=\sqrt{\frac{T}{\mu}}}\) (推導方法從略)
其中 \(T\) 為軟彈簧上張力、\(\mu \) 為彈簧的線性質量密度。它們對波速的影響為:
舉例說,有兩根長度相等的軟彈簧(),質量較大的一根,便有較高的線性密度。若兩根軟彈簧都被大小相同的張力拉長,質量較大的軟彈簧上的波,波速便較低。總結而言,以上雖僅以軟彈簧的情況來說明,但對於機械波:
影響波速的因素,是介質的特性(軟彈簧的情況就是彈簧張力和線性質量密度),不是波的振幅和頻率!
