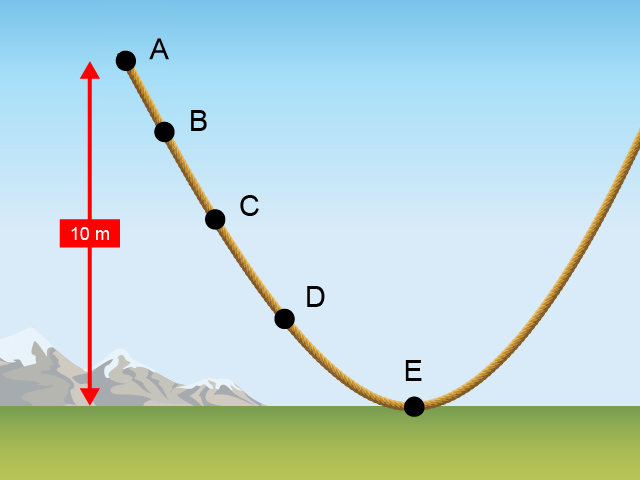
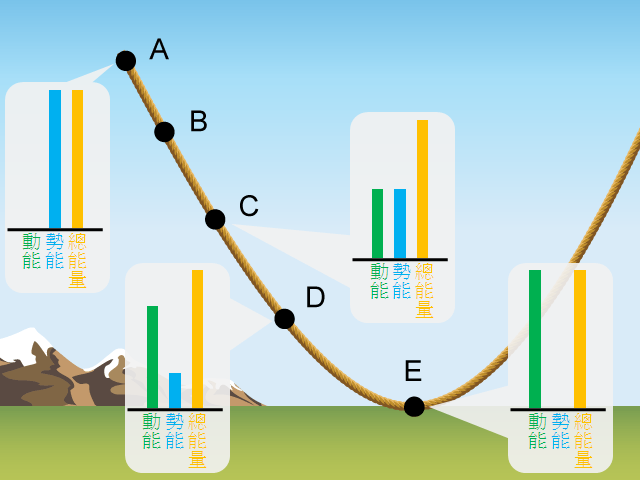
你玩過滑板嗎?你知道有一種滑板運動,是滑板者在 U 型台上運動和做出動作嗎()?當滑板者於 U 型台兩端之間來回運動,便體現了動能與勢能的相互轉移。裡所示為一個典型 U 台的側視圖。忽略地面摩擦與空氣阻力等因素,當滑板者在 U 台上來回運動時,總能量會維持不變。而滑板者位於 U 台上不同位置時,動能與勢能便有不同的分佈,如下方各棒型圖所示:

設 U 台的末端跟地面之間的垂直高度為 \(h\) = 10 \(\text{m}\)(),那麼,我們可以找出滑板者於 U 台上的運動速率可以有多大嗎?當滑板者位於點 E 時,所有的勢能已轉化為動能,即有最大的速率 (設為 \(v\));而滑板者位於點 A 時,所有的動能已轉化為勢能,處於瞬時靜上狀態。由於總能量不變,即滑板者:
於 E 點動能 + 於 E 點勢能 \(=\) 於 A 點動能 + 於 A 點勢能
\(\tfrac{1}{2}m{{v}^{2}}+0=0+mgh\)
上式中 \(m\) 和 \(g\) 分別是滑板者的質量和重力加速度 (\(9.8\ \text{m}\ {{\text{s}}^{-2}}\))。換言之,\(v\) = \(\sqrt{2gh}\)。代入數字後便可算出 \(v\) = \(14\ \text{m}\ {{\text{s}}^{-1}}\)。
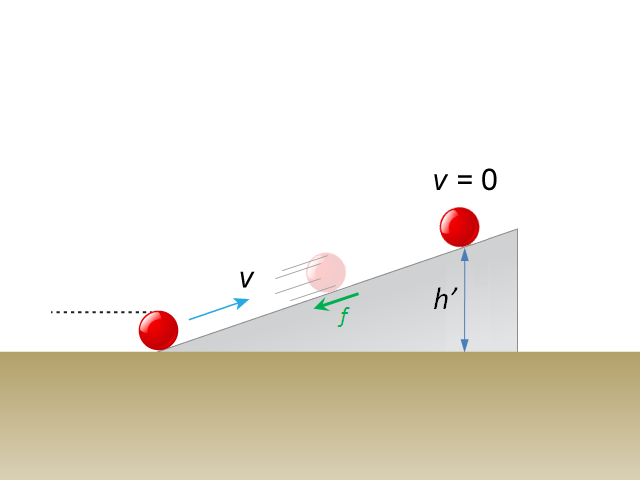
如所示,質量為 1 \(\text{kg}\) 的小球向傾斜角等於 \(28{}^\circ \) 的斜坡從下向上運動。起初,小球位於斜坡的最低點時有速率 \(3.0\ \text{m}\ {{\text{s}}^{-1}}\)。隨着小球向上移,其運動愈來愈慢。當小球的速率等於零,其位置與地面之間的垂直距離為 \(h\)。忽略小球與斜坡之間的摩擦力及其他阻力,如何求解小球沿斜面爬行的距離呢?
要找出小球沿斜面所移動的距離,可以先求 \(h\),之後再運用三角幾何計算小球的移動距離。設以符號 \(s\) 和 \(v\) 分別表示小球的垂直位移和瞬時速率,即當 \(s\) = 0,小球位於斜坡最低點、\(v\) = \(3.0\ \text{m}\ {{\text{s}}^{-1}}\);當 \(s\) = \(h\),小球在斜坡上瞬時靜止、\(v\) = 0。以 \(K\) 和 \(U\) 分別代表動能與重力勢能,根據機械能守恆:
\({{K}_{s=0}}+{{U}_{s=0}}={{K}_{s=h}}+{{U}_{s=h}}\)
\(\tfrac{1}{2}m{{v}^{2}}+0=0+mgh\)
上式中 \(m\) 和 \(g\) 分別是小球的質量和重力加速度 (\(9.8\ \text{m}\ {{\text{s}}^{-2}}\))。換言之,\(h\) = \({{{v}^{2}}}/{2g}\;\)。代入數字後便可算出 \(h\) = 0.46 \(\text{m}\)。而小球沿斜面的移動距離就是 \({h}/{\sin 28{}^\circ }\;\),即 0.98 \(\text{m}\)。
再進階考慮,如果加入摩擦力的因素,結果會否不同呢?請按「考慮摩擦力」看有關敘述!
若本情境改為小球沿斜面運動時,固定的摩擦力 \(f\) 會作用於小球上()。另假設 \({h}'\) = 0.9 \(h\),以下我們嘗試估計 \(f\) 的大小。
摩擦力作用於小球上,會令小球於運動過程中損失機械能。換言之,本情況中小球的總機械能不再守恆。我們先寫出小球位於 \(s\) = 0 和 \(s\) = \({h}'\) 的總機械能:
\({{K}_{s=0}}+{{U}_{s=0}}=\tfrac{1}{2}m{{v}^{2}}+0=\tfrac{1}{2}m{{v}^{2}}\)
\({{K}_{s={h}'}}+{{U}_{s={h}'}}=0+mg{h}'=0.9\ mgh\)
上方兩式的相差,就是機械能的損耗。這損耗便等於摩擦力對小球所作的負功,而 \(f\) 作功的位移等於 \({{{h}'}}/{\sin 28{}^\circ }\;\):
\(f\left( {{{h}'}}/{\sin 28{}^\circ }\; \right)=\tfrac{1}{2}m{{v}^{2}}-0.9\ mgh\)
代入 \({h}'\) = 0.9 \(h\)、\(h\) = 0.46 \(\text{m}\)、\(m\) = 1 \(\text{kg}\)、\(v\) = \(3\ \text{m}\ {{\text{s}}^{-1}}\),求得 \(f\) \(\approx \) 0.5 \(\text{N}\)。