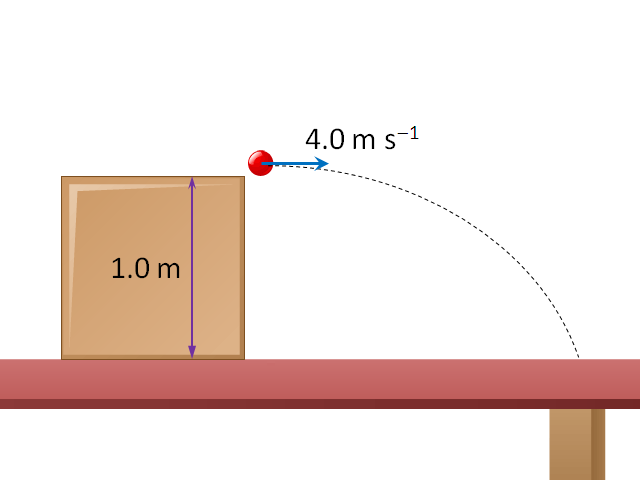
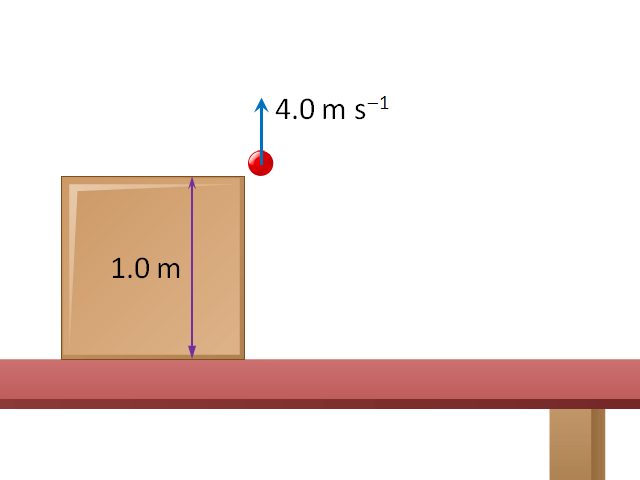
如所示,小球 A 以初速率 \(4.0\ \text{m}\ {{\text{s}}^{-1}}\) 在桌面以上 1.0 \(\text{m}\) 高的所在被水平拋出。之後,小球會循一條拋物線的路徑運動,最終會落地(抵達桌面)。質量和大小皆與小球 A 相同的小球 B,在同一設置和所處高度被上拋,如所示,初速率同為 \(4.0\ \text{m}\ {{\text{s}}^{-1}}\)。忽略空氣阻力,試找出小球 A 和小球 B 落地時的速率。(設重力加速度為 \(g\) = \(9.8\ \text{m}\ {{\text{s}}^{-2}}\))
【題解】
考慮桌面為參考點。設小球質量為 \(m\)、起初所處高度為 \(h\)、初速率為 \(u\)、抵達桌面時速率為 \(v\)。小球剛拋出時,小球的總能量包含動能和勢能;小球剛抵達桌面時,小球的總能量只包含動能、沒有勢能。由於總能量不變,可寫出:
\(\tfrac{1}{2}m{{u}^{2}}+mgh=\tfrac{1}{2}m{{v}^{2}}+0\)
即 \(v=\sqrt{{{u}^{2}}+2gh}\)。代入 \(u\) = \(4.0\ \text{m}\ {{\text{s}}^{-1}}\)、\(h\) = 1.0 \(\text{m}\),求得 \(v\) = \(6.0\ \text{m}\ {{\text{s}}^{-1}}\)。
本例的重點為,上方的整套分析和計算,不但適用於小球 A 的平拋情境(),亦同樣適用於小球 B 的上拋情境()。為何兩情境的設置不一樣,解題卻相同呢?由於以能量方法處理時,無需關注運動的路徑。再者,小球 A 和小球 B 的最初垂直高度和初速率是相同的(兩者都是 1.0 \(\text{m}\) 和 \(4.0\ \text{m}\ {{\text{s}}^{-1}}\)),故兩者總能量也是一樣的。當它們抵達桌面時,必定有同等的動能和速率。
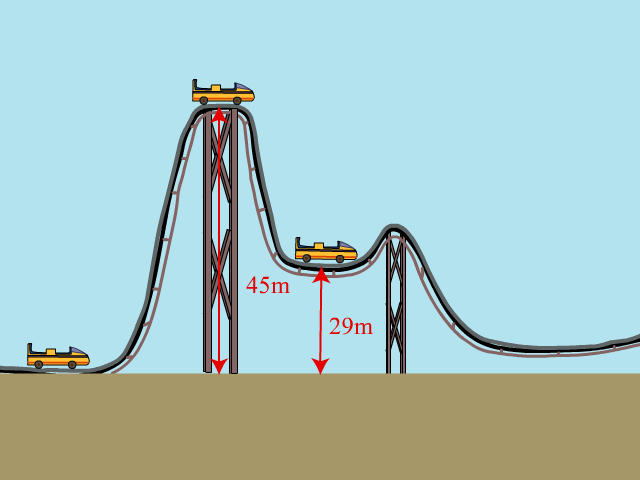
一架 500 \(\text{kg}\) 的過山車被鏈條拖到 45 \(\text{m}\) 的最高處。到達最高處時,過山車的速率是零。忽略摩擦力,求 (a) 鏈條要做多少功才能使過山車到達最高處?(b) 過山車跑回 45 \(\text{m}\) 下的地面時,過山車的速率是多少?(c) 當過山車跑到離地面 29 \(\text{m}\) 時,過山車的速率是多少?(設重力加速度為 \(g\) = \(9.8\ \text{m}\ {{\text{s}}^{-2}}\))
鏈條對過山車所做的功會轉化為過山車的勢能。過山車獲得的勢能,就是於 45 \(\text{m}\) 高處(點 A)的勢能減去於地面的勢能(設為零)。故鏈條的作功:
\(W=mgh-0=\left( 500\ \text{kg} \right)\left( 9.8\ \text{m}\ {{\text{s}}^{-2}} \right)\left( 45\ \text{m} \right)=220500\ \text{J}\)
根據能量守恒定律,當過山車跑回 45 \(\text{m}\) 下的地面時,它在 45 \(\text{m}\) 高處獲得的勢能,會全部轉化為動能,即:
\(220500\ \text{J}=\tfrac{1}{2}m{{v}_{gnd}}^{2}\)
代入 \(m\) = 500 \(\text{kg}\) 便求得過山車回到地面的速率 \({{v}_{gnd}}\) = \(30\ \text{m}\ {{\text{s}}^{-1}}\)。
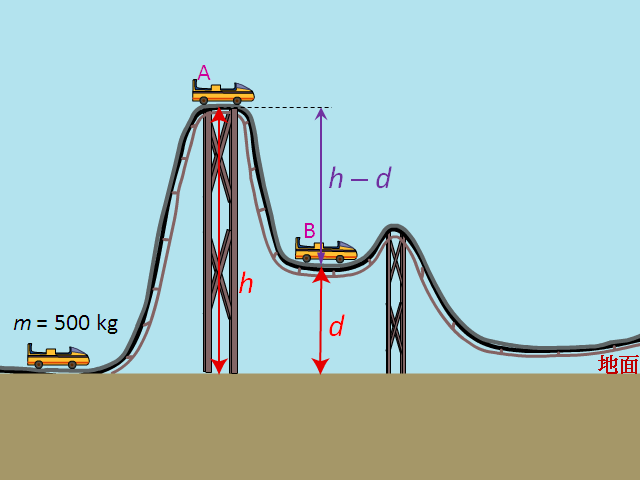
根據能量守恒,過山車從 \(h\) 跑到離地面 \(d\) = 29 \(\text{m}\) 的高度時(點 B),即其勢能變化爲 \(mg\left( h-d \right)\)。而這勢能變化會全部轉化爲過山車的動能,則有:
\(mg\left( h-d \right)=\tfrac{1}{2}m{{v}_{B}}^{2}\)
代入 \(h-d\) = 16 \(\text{m}\),求得過山車於點 B 時的速率 \({{v}_{B}}\) = \(17.71\ \text{m}\ {{\text{s}}^{-1}}\)。
與之前的問題 (c) 類似,但改為當過山車被鏈條拖到 45 \(\text{m}\) 的最高處後,考慮速率並非零、而是 \(4\ \text{m}\ {{\text{s}}^{-1}}\)。當過山車跑到離地 29 \(\text{m}\) 所在時(點 B),過山車的速率是多少?
【題解】
設符號如中所示。過山車在最高點(點 A)時的機械能,等於過山車在該位置時的動能和勢能之和:\(\tfrac{1}{2}m{{v}_{A}}^{2}+mgh\)。而過山車跑到離地面 \(d\) 的位置(點 B)時,其機械能亦包括動能與勢能:\(\tfrac{1}{2}m{{v}_{B}}^{2}+mgd\)。由於過山車的總能量守恆,可寫出:
\(\tfrac{1}{2}m{{v}_{A}}^{2}+mgh=\tfrac{1}{2}m{{v}_{B}}^{2}+mgd\)
即 \({{v}_{B}}\) = \(\sqrt{{{v}_{A}}^{2}+2g\left( h-d \right)}\)。代入 \({{v}_{A}}\) =\(4\ \text{m}\ {{\text{s}}^{-1}}\)、\(h-d\) = 16 \(\text{m}\),運算後求得 \({{v}_{B}}\) =\(18.15\ \text{m}\ {{\text{s}}^{-1}}\)。