速度 (velocity) 能一次過指出物體運動的快慢及方向,是每個單位時間內物體的位移變化。
| 符號 | 定義 | 單位(符號) | 標量/矢量? |
|---|---|---|---|
| \(v\) | 位移的變化率 \(\displaystyle{v=\frac{\text{位移變化}}{\text{所用時間}}}\) | \(\text{m}\ {{\text{s}}^{-1}}\) | 矢量 |
平均速率與瞬時速率必定是正值,因為它們沒有考慮物體移動的方向。速度則能一次過指出物體運動的快慢和方向。
某運動物體的平均速度 (average velocity) 就是總位移變化 (\(\Delta s\)) 除以所用總時間 (\(\Delta t\)):
平均速度 \(\displaystyle{\bar{v}=\frac{\Delta s}{\Delta t}}\)
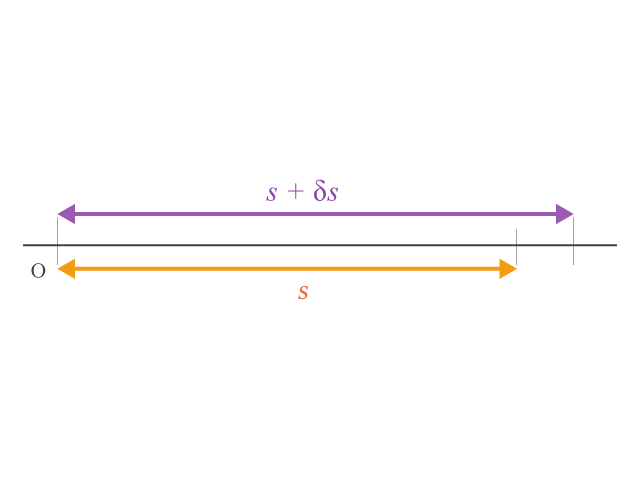
同樣地,如所示,物體在某時間 \(t\) 的瞬時速度 (instantaneous velocity) 則是位移變化 (\(\delta s\)) 除以所用時間 (\(\delta t\)):
瞬時速度 \(\displaystyle{v=\frac{\delta s}{\delta t}}\)
很多時,瞬時速度會乾脆叫作速度。留意速率和速度均以符號「\(v\)」表示。
速度有甚麼符號?它們會代表甚麼呢?
你可在改變速度的大小和正負號,演示車子的運動,藉此探究速度方向與車子運動的關係。
考慮向右為正,試從模擬結果找出速度正負與位移的關係,在下方選擇正確的項目:
【題解】 由於已假設向右為正,所以車子移向右時 \(v > 0\);移向左則 \(v < 0\)。
與速率不同,速度可正可負。所以瞬時速度定義中的 \(\delta s\),亦可正可負。換言之,
當 \(v > 0\),可知 \(\delta s > 0\),表示位移增加;
當 \(v < 0\),可知 \(\delta s < 0\),表示位移減少。
請閱讀下方的例子,掌握速率與速度的概念和分別。
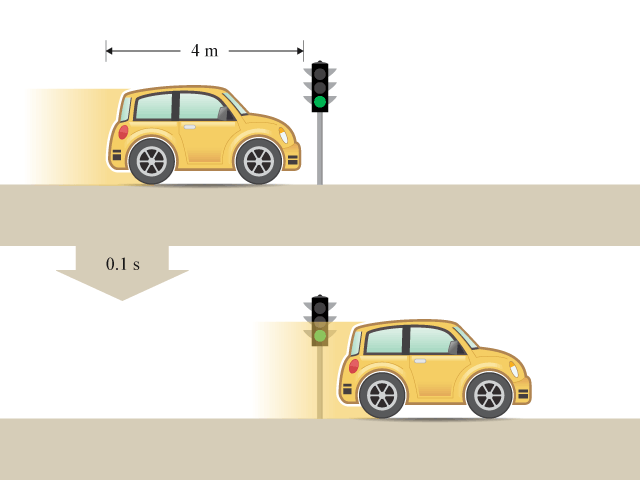
一輛全長 \(4 \text{ m}\) 的汽車向右行駛,汽車需時 \(0.10\) 秒以通過路上一盞紅綠燈(見)。若設向左為正,這時汽車的速率和速度為若干?
考慮:
速率 = \(\displaystyle{\frac{\delta s}{\delta t}}\)
\(\delta t\) 乃很短的時間間距。由於時間 \(0.10\) 秒可算是一足夠短的時間間距,換言之:
速率 = \(\displaystyle{\frac{4\ \text{m}}{0.1\ \text{s}}=40\ \text{m}\ {{\text{s}}^{-1}}}\)
由於速率就是速度的量值,而汽車的運動方向為向右,所以
速度 = \(−40 \text{ m}\ {{\text{s}}^{-1}}\)
一輛汽車從 \(\text{O}\) 開始在一條直路上向右行駛了 \(20 \text{ km}\)。接着汽車折返 \(\text{O}\) 點,全程花了一小時。求該汽車的平均速率與平均速度。
汽車從 \(\text{O}\) 點出發行了 \(20 \text{ km}\) 後便沿原路折返,換言之:
所行總距離 = \(40 \text{ km}\) 位移變化 = \(0 \text{ km}\)
考慮:
\(\begin{align} \text{平均速率} &= \text{所行總距離} / \text{所用總時間} = 40 \text{ km} / 1 \text{ hr} \\ &= 40 \text{ km}\ {{\text{h}}^{-1}}\end{align}\)
\(\begin{align} \text{平均速度} &= \text{位移變化} / \text{所用總時間} = 0 \text{ km} / 1 \text{ hr} \\ &= 0 \text{ km}\ {{\text{h}}^{-1}}\end{align}\)
若你對速率和速度概念的掌握仍沒信心,可嘗試完成下方的問題,鞏固之前所學內容: