當矢量相加時，合矢量的大小，不一定等於所有矢量大小之總和的。矢量相加方法有很多，在這裏我們先學習最簡單的首尾連接法（見和）。

首尾連接法的步驟如下：

1. 移動其中一個矢量，把它的始點連接到另一個矢量的終點；
2. 繪出一個從後一個矢量的始點，指向前一個矢量的終點之箭號。該箭號就是兩個矢量之總和。

而矢量之和，稱為合矢量。用首尾連接法繪出合矢量後，我們可以利用尺和量角器測量合矢量的大小和方向。

若果相加的矢量超過兩個，我們亦可用首尾連接法先把所有矢量連成一串，再繪出合矢量，如所示。

如未相加前的矢量方向相同、相反或互相垂直，就可以運用數學幾何方法，計算合矢量的大小和方向。現在以位移為例子，示範矢量相加。

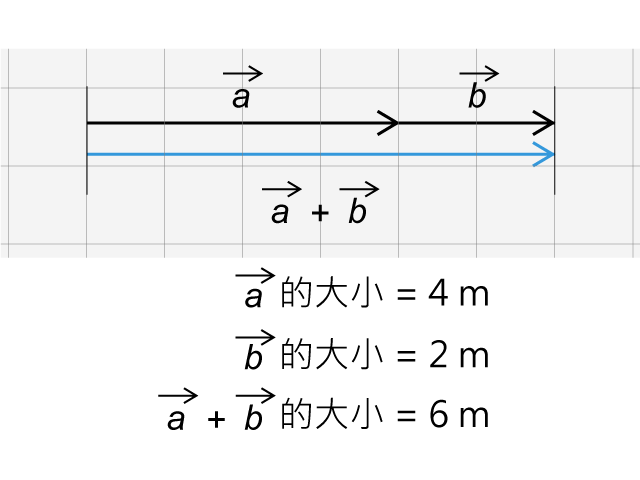
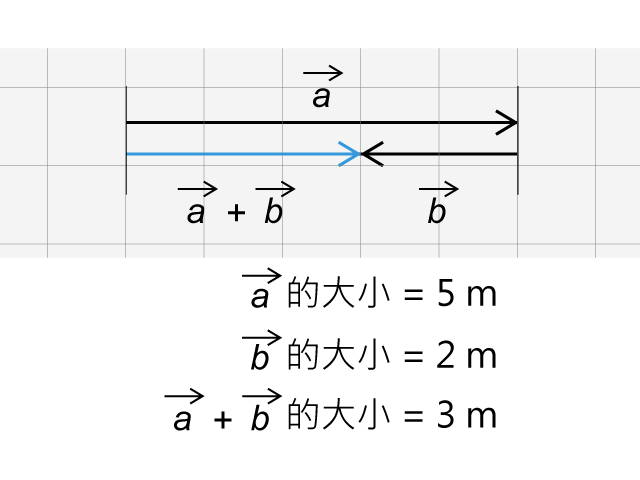
如果所有矢量都是在同一直線上，或互相平行，只要先繪出合矢量，了解情況後，再把矢量的大小相加或相減，就能得到合矢量的大小。例如：

• 在，位移 \(\text{a}\) 及位移 \(\text{b}\) 的方向相同，其合位移的大小為 \(4 \text{ m} + 2 \text{ m} = 6 \text{ m}\)；
• 在，位移 \(\text{a}\) 及位移 \(\text{b}\) 的方向相反，其合位移的大小為 \(5 \text{ m} − 2 \text{ m} = 3 \text{ m}\)。

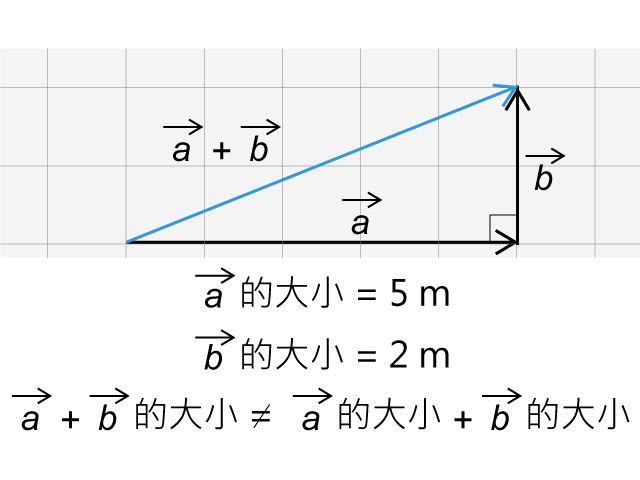
如果兩個位移是互相垂直的，如所示，很明顯，合位移的大小，不等於位移 \(\text{a}\) 的大小加位移 \(\text{b}\) 的大小。在這情況下，便要用三角函數及畢氏定理找出合位移的大小及方向了。

就說明了計算的方法。