試想像，在筆直的路軌上有一列火車，該火車只可以向觀察者的左方或右方運動。在這情況下，用正負號便足以表示火車的運動方向。

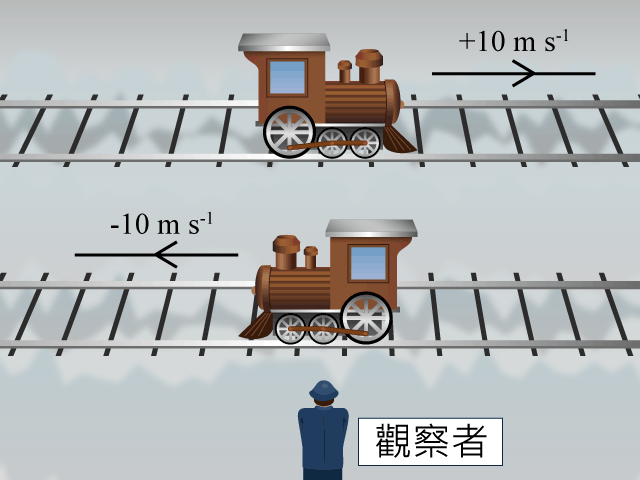
設向右為正方向(+)，那麼向左便是負方向(−)。舉例說，一輛速率為 \(10 \text{ m}\ {{\text{s}}^{-1}}\) 的火車頭，如它：

• 向右駛，其速度便是 \(+10 \text{ m}\ {{\text{s}}^{-1}}\)；
• 向左駛，其速度便是 \(−10 \text{ m}\ {{\text{s}}^{-1}}\)。

當一隻甲蟲在葉面上走動時，它除了可以前後移動外，還可以向左右或其他方向移動。在這情況下，只用正負號不足以表示甲蟲的運動方向。要描述這甲蟲的速度，便要用矢量的表示方法了。

矢量包含了方向和量值。我們可以用箭號來表示矢量（）：

• 箭號長度表示矢量的大小；
• 箭號方向表示矢量的方向。

矢量箭號的箭頭，稱為終點；箭號的末端，稱為始點。

為了指明速度是一個矢量，會用符號 \(\vec{v}\) 表示。字母 \(v\) 上的箭號表示 \(v\) 是一個矢量。為了方便電腦輸入，會把 \(\vec{v}\) 記作「矢量 \(v\)」。