為要描述物體運動的快慢,運動學上定義了速率 (speed) 。
| 符號 | 定義 | 單位(符號) | 標量/矢量? |
|---|---|---|---|
| \(v\) | 距離的變化率 \(\displaystyle{v=\frac{\text{移動距離}}{\text{所用時間}}}\) | \(\text{m}\ {{\text{s}}^{-1}}\) | 標量 |
若某物體在總時間 \(T\) 內的所行總距離等於 \(X\),物體的平均速率 (average speed) 可定義為:
平均速率 \(\displaystyle{\bar{v}=\frac{X}{T}}\)
【例子】
考慮一輛車子行走了一段時間,如 \(50\) 分鐘。若車內的里程表顯示這 \(50\) 分鐘內行走了 \(30 \text{ km}\)(見),試計算車子的平均速率。
根據平均速率定義:
\(\begin{align} \bar{v} &= \frac{X}{T}=\frac{30\ \text{km}}{50\ \text{min}} \\ &= 0.6\ \text{km}\ \text{mi}{{\text{n}}^{-1}} \\ &= 0.6\ \frac{1000\ \text{m}}{60\ \text{s}} \\ &= 10\ \text{m}\ {{\text{s}}^{-1}}\end{align}\)

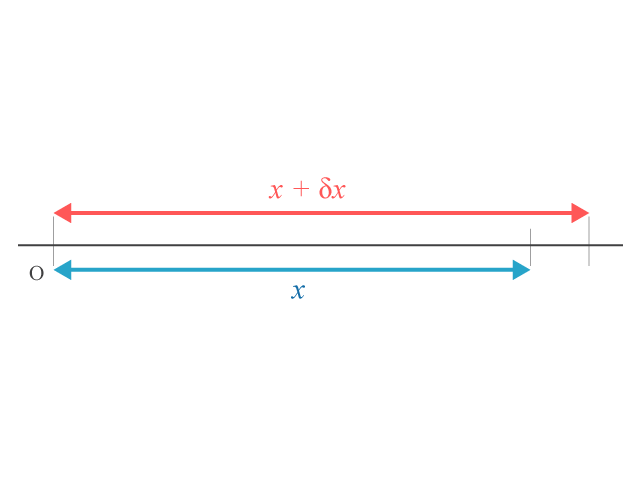
速率的定義為車子在一個很短的時間間距內所行走的微小距離。若有關距離和時間間距分別是 \(\delta x\) 和 \(\delta t\),如所示,瞬時速率 (instantaneous speed) 等於
瞬時速率 \(\displaystyle{v=\frac{\delta x}{\delta t}}\)
符號 \(\delta \) 代表該微量的改變,以微積分表示時
瞬時速率 \(\displaystyle{v=\frac{\delta x}{\delta t}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta x}{\Delta t}}\)
留意速率必定為正數。很多時,瞬時速率會乾脆叫作速率。
【例子】
一輛全長 \(4.2 \text{ m}\) 的汽車在一條直路上行走,它需時 \(0.56\) 秒以通過路上一個標記。汽車的速率等於多少?
根據速率的定義:
\(\begin{align} v &= \frac{\delta x}{\delta t}=\frac{4.2\ \text{m}}{0.56\ \text{s}} \\ &= 7.5\ \text{m}\ {{\text{s}}^{-1}}\end{align}\)
中設置了三個例子,根據指示回答問題後,可讓你進一步了解平均速率與瞬時速率的區別。
設三個例子中的平均速率分別是 \({{\bar{v}}_{1}}\)、\({{\bar{v}}_{2}}\) 和 \({{\bar{v}}_{3}}\)。請在下方選擇正確的答案。
【題解】 完成播放後,三個例子的車子皆在 \(5 \text{ s}\) 內行走了 \(50 \text{ m}\),所以它們有相同的平均速率。
根據模擬結果,哪些例子的瞬時速率在旅程中會起變化?
(1)範例 \(1\)
(2)範例 \(2\)
(3)範例 \(3\)
【題解】
總括而言,三個範例雖有相同的平均速率,但車子在該段時間內有時可能跑得較平均速率快、有時卻跑得較平均速率慢(範例 \(1\) 和 \(3\) 屬勻速率運動)。用平均速率來描述運動其實是一個比較粗略的方法。
汽車都配備了一個速率計的儀器(見),它會顯示車子在一個時間瞬間的速率。我們稱速率計讀取了汽車的瞬時速率。
