你可開啟下方的內容進行活動,根據指示操作模擬程式,探究位移 (displacement) 的概念。
簡言之,位移 (displacement) 的概念可歸納如下:
| 符號 | 定義 | 單位(符號) | 標量/矢量? |
|---|---|---|---|
| \(s\) | 在特定方向上移動的距離,用以描述物體位置變動的物理量。 | 米 (\(\text{m}\)) | 矢量 |
顯示質點相對於 \(\text{O}\) 點的距離 (distance) 和位移 (displacement)。試根據模擬結果在下方選擇正確的答案:
【題解】 若有一個相對於 \(\text{O}\) 點的位移,它的量值就是距離,其符號則告訴我們質點位於 \(\text{O}\) 的左方還是右方。
位移是向量,繪圖時會以箭號表示(見模擬程式)。在直線運動中表示位移時,可用其量值來表示距離,用正負號來表示方向。再者,位移很多時會用符號 \(s\) 表示(多維的情況用 \(\vec{r}\) ),並取 \(\text{O}\) 的右方為正的位移;\(\text{O}\) 的左方為負的位移。
當要表示位移的變化 (\(\Delta s\)) 時,就是:
\(\text{位移變化} \Delta s = \text{最终位移} − \text{起始位移}\)
若物體的運動不在同一直線上,我們也可用位移來表示物體位置的變化:
位移包括量值和方向。當物體的運動不在同一直線上,位移方向便不能僅用正負號來區分。象限角法就是一種表示位移方向的形式。試回答下方的問題學習象限角法。
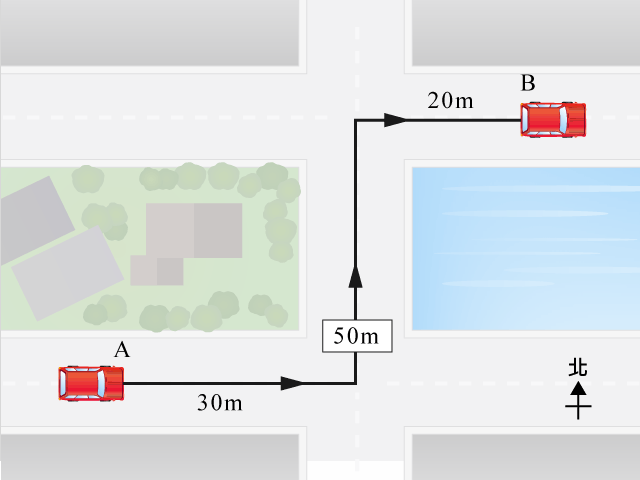
如所示,一輛車從 \(\text{A}\) 點出發,先向東行駛 \(30 \text{ m}\),然後向北行 \(50 \text{ m}\),再向東行 \(20 \text{ m}\),到達 \(\text{B}\) 點。這輛車的位移是多少?
A. \(70.7 \text{ m} (\text{N } 45°\text{E})\)
B. \(70.7 \text{ m} (\text{S } 45°\text{W})\)
C. \(100 \text{ m} (\text{N } 45°\text{E})\)
D. \(100 \text{ m} (\text{S } 45°\text{W})\)
【題解】 要找出車子的位移,需計算 \(\text{A}\) 點及 \(\text{B}\) 點間的直線距離,以及 \(\text{B}\) 點相對於 \(\text{A}\) 點的方向。圖中藍色箭咀為車子位移:
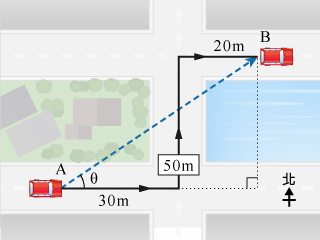
利用畢氏定理:
\(\text{AB}^{2} = (50 \text{ m})^{2} + (20 \text{ m} + 30 \text{ m})^{2} \\ \Rightarrow \text{ AB} = 70.7 \text{ m}\)
利用三角幾何:
\(\tan \theta = 50 \text{ m} / (20 \text{ m} + 30 \text{ m}) \\ \Rightarrow \theta = 45°\)
當以象限角法表示方位,位於第一或第二象限時,角度便由北方開始計算,換言之,車子位移為 \(70.7 \text{ m}(\text{N } 45°\text{E})\)。反之,若方位處於第三或第四象限時,角度便由南方開始計算。
之前在「體驗位移」的活動中,乃假設了質點運動的起始位置是 \(\text{O}\)、過程中沒有改變方向。然而,若物體的運動包含多個不同方向的段落,如何計算位移呢?
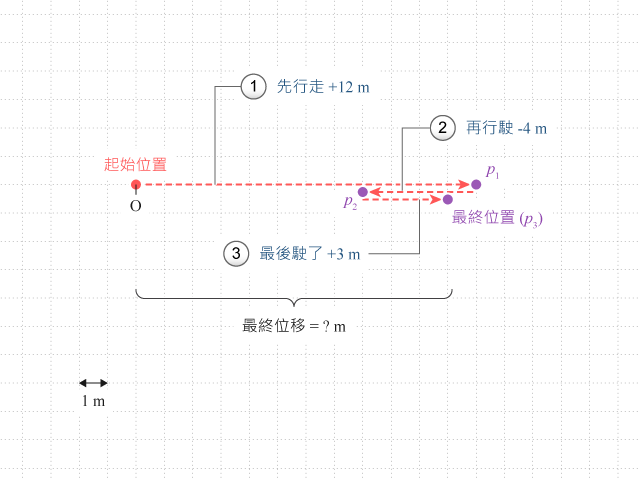
例如一輛車子從點 \(\text{O}\) 行走了 \(+12 \text{ m}\) 的位移至某點(設該點 \(p_{1}\)),然後從 \(p_{1}\) 行駛 \(-4 \text{ m}\) 的位移(設到達 \(p_{2}\)),最後再從 \(p_{2}\) 駛了 \(+3 \text{ m}\) 的位移(設到達 \(p_{3}\))。試計算車子最終的位移。
你可打開下方內容,根據指示先利用運動與線圖模擬程式演示有關運動,尋找答案:
【題解】
當物體的運動包含多個段落,物體的位移變化 (\(\Delta s\)) 就是各段落位移的相加。在本例中車子運動包含 \(3\) 個段落,換言之:
\(\begin{align}\Delta s &= \text{O 至 }p_{1} \text{ 位移} + p_{1} \text{ 至 } p_{2} \text{ 位移} + p_{2} \text{ 至 } p_{3} \text{ 位移} \\ &= 12 \text{ m} + (-4 \text{ m}) + 3 \text{ m} \\ &= 11 \text{ m}\end{align}\)
車子的起始位置在 \(\text{O}\) 點,所以起始位移是 \(0\)。
\(\begin{align} \text{ 車子的最终位移} &= \Delta s + \text{車子的起始位移} \\ &= 11 \text{ m} + 0 \text{ m} \\ &= 11 \text{ m}\end{align}\)
請閱讀下方的例子,掌握距離與位移的概念和分別。
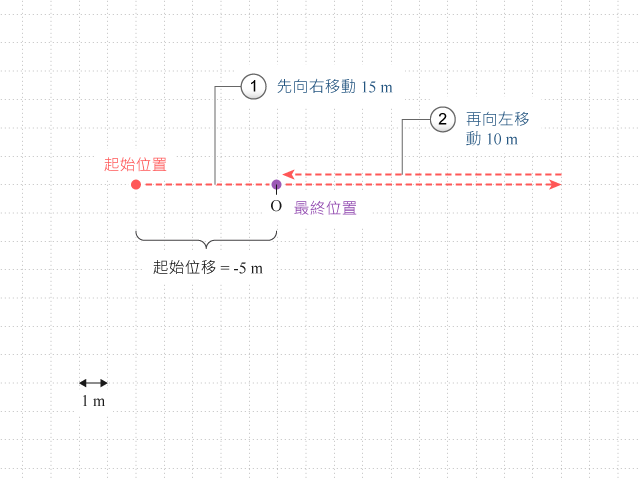
某物體有一個 \(−5 \text{ m}\) 的位移。它首先向右移動 \(15 \text{ m}\),然後向左移動 \(10 \text{ m}\)。設向右為正,顯示物體在過程中的路徑。試計算運動物體的行走距離、位移變化、以及最終位移
【題解】
\( \ \ \text{物體所行總距離} = 15 \text{ m} + 10 \text{ m} = 25 \text{ m}\)
\(\begin{align}\text{ 物體的位移變化} &= \text{各段落位移的相加} \\ &= 15 \text{ m} + (−10 \text{ m}) = 5 \text{ m}\end{align}\)
起初,物體有一個 \(−5 \text{ m}\) 的位移,所以始位移等於 \(−5 \text{ m}\)。換言之:
\(\begin{align}\text{ 物體的最終位移} &= \text{ 位移變化} + \text{起始位移} \\ &= 5 \text{ m} + (−5 \text{ m}) = 0 \text{ m}\end{align}\)
你可在運動與線圖模擬程式先設定始位移,然後拖放車子右移 \(15 \text{ m}\)、左移 \(10 \text{ m}\),來驗證本題的答案。
若你對距離和位移概念的掌握仍沒信心,可嘗試完成下方的問題,鞏固之前所學內容: