如果物體在 \(\Delta t\) 時間內，其角速度由 \(\omega \) 變到 \(\omega +\Delta \omega \)，那麼物體在 \(\Delta t\) 時間內的平均角加速度 (average angular acceleration) 定義為：

\(\displaystyle{\bar{\alpha }=\frac{\Delta \omega }{\Delta t}}\)

角加速度的單位是 \(\text{rad}\ {{\text{s}}^{-2}}\)。當平均角加速度中的 \(\Delta t\) 很小時，就是瞬時角加速度 \(\alpha \) (instantaneous angular acceleration)：

\(\displaystyle{\alpha =\frac{\delta \omega }{\delta t}}\)

在勻速圓周運動中，角加速度 \(\alpha =0\)。

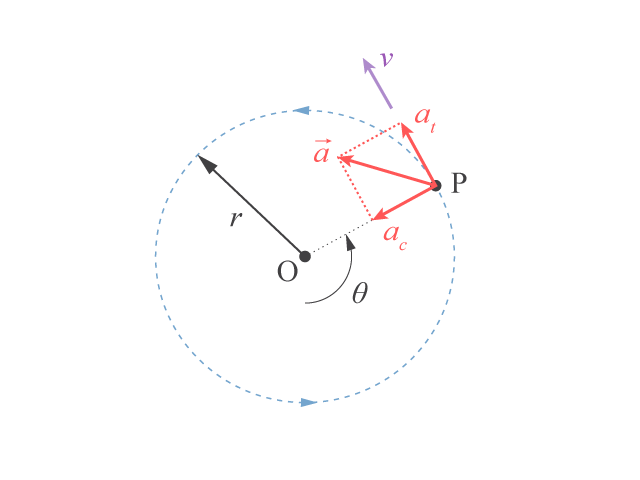
在非勻速圓周運動中，向心加速度仍然存在。另一方面，在物體運動的方向上還有切向加速度 (tangential acceleration)，如所示。換言之，物體的加速度就是：

\(\begin{align} \vec{a} &= \frac{\delta v}{\delta t}\hat{t}+\frac{{{v}^{2}}}{r}\hat{n} \\ &= r\alpha \ \hat{t}+r{{\omega }^{2}}\ \hat{n}\end{align}\)

單位向量 \(\hat{t}\) 和 \(\hat{n}\) 分別沿運動方向和指向圓形軌道的圓心。