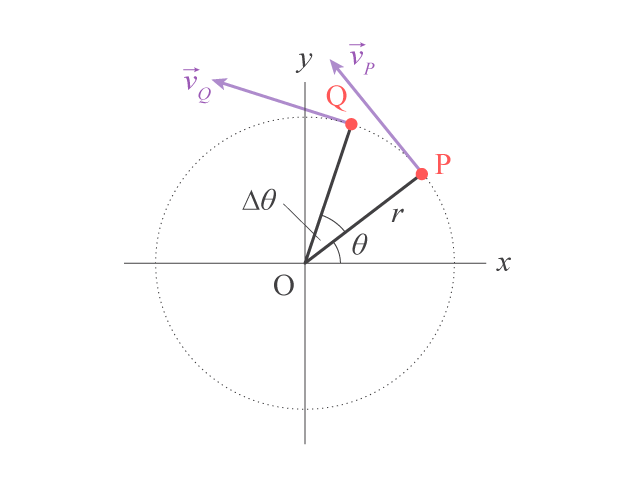
考慮某物體繞固定軸（垂直螢幕向外）作圓周運動，如所示。若在 \(t\) 時刻，物體位於 \(\rm{P}\) 點，半徑 \(r\) 與 \(x\) 軸成 \(\theta \) 角，在 \(t+\Delta t\) 時刻，物體到達 \(\rm{Q}\) 點，半徑 \(\rm{OQ}\) 與 \(x\) 軸成 \(\theta +\Delta \theta \) 角，則 \(\Delta \theta \) 稱為在 \(\Delta t\) 時間內物體的角位移 (angular displacement)。

為了描述物體作圓周運動的快慢程度，平均角速度 (average angular velocity) 定義為

\(\displaystyle{\bar{\omega }=\frac{\Delta \theta }{\Delta t}}\)

當平均角速度中的 \(\Delta t\) 很小時，就是瞬時角速度 \(\omega \) (instantaneous angular velocity)：

\(\displaystyle{\omega =\frac{\delta \theta }{\delta t}}\)

角速度是向量，單位為 \(\text{rad}\ {{\text{s}}^{-1}}\)，包括量值和方向（順時針或逆時針）。若不用考慮運動方向，可以使用角速率 (angular speed)。在勻速圓周運動中，\(\omega \) 是常數，所以上式可以寫成：

\(\displaystyle{\omega =\frac{\theta }{t}}\)

式中 \(\theta \) 與 \(t\) 分別代表角位移的變化和所需時間。