[興倫智能課堂] 電荷

庫倫定律的形式，與描述作用於兩質點間的重力的牛頓萬有引力定律相同（）。我們可以把庫倫定律：

\(\displaystyle{{{F}_{coul}}=k\frac{{{Q}_{1}}\ {{Q}_{2}}}{{{r}^{2}}}}\)

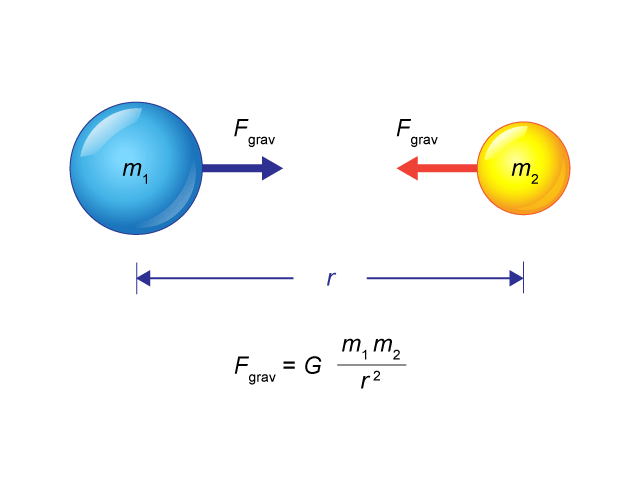
與萬有引力定律：

\(\displaystyle{{{F}_{grav}}=G\frac{{{m}_{1}}\ {{m}_{2}}}{{{r}^{2}}}}\)

作對比，方便記憶和應用：

在庫倫定律與萬有引力定律中，力與質點間距離都具有平方反比的關係 (\(F\propto {{r}^{-2}}\))；
庫倫定律中的比例常數 \(k\)，可以類比於萬有引力定律中的重力常數 \(G\)。

概念鞏固

牛頓萬有引力定律

	庫倫定律	萬有引力定律
公式	\(\displaystyle{{{F}_{coul}}=k\frac{{{Q}_{1}}\ {{Q}_{2}}}{{{r}^{2}}}}\)	\(\displaystyle{{{F}_{grav}}=G\frac{{{m}_{1}}\ {{m}_{2}}}{{{r}^{2}}}}\)
意義	一個質點由於帶電而施加於另一質點上的力	任何兩質點之間均存在的互相吸引的力
參數	與兩個物體的相距和質量重量所帶電荷量有關	與兩個物體的相距和質量重量所帶電荷量有關
力的性質	必定是吸力必定是斥力可以是吸力或斥力	必定是吸力必定是斥力可以是吸力或斥力

【題解】
由於 \({{Q}_{1}}\) 和 \({{Q}_{2}}\) 的乘積可正可負，所以 \({{F}_{coul}}\) 可以是吸力或斥力；

然而 \({{m}_{1}}\) 和 \({{m}_{2}}\) 的乘積必為正數，留意 \({{F}_{grav}}\) 必定是吸力。

【問題 \(1\)】
氫原子中電子與質子（在原子核內）之間的距離，在最低能量狀態下為 \(r = 0.529 \times 10^{-10} \ \text{m}\)。（引力常量 \(G = 6.67 \times 10^{−11} \ \text{N}\ {{\text{m}}^{2}}\ \text{k}{{\text{g}}^{-2}}\)，電子質量 \({{m}_{e}} = 9.1 \times 10^{−31} \ \text{kg}\)，質子質量 \({{m}_{p}} = 1.67 \times 10^{−27} \ \text{kg}\)）

分別計算它們之間的靜電力和萬有引力，可知在氫原子中質子與電子間...

動畫 \(1\)：氫原子

【題解】
設 \({{Q}_{p}}\) 和 \({{Q}_{e}}\) 分別是質子和電子的所帶電量，根據庫倫定律，它們之間的靜電力 \({{F}_{coul}}\) 等於：

\(\displaystyle{{{F}_{coul}}=k\frac{{{Q}_{p}}\ {{Q}_{e}}}{{{r}^{2}}}}\)
\(\displaystyle{\begin{align} & =\left( 9\times {{10}^{9}} \right)\frac{\left( 1.6\times {{10}^{-19}} \right)\left( -1.6\times {{10}^{-19}} \right)}{{{\left( 0.529\times {{10}^{-10}} \right)}^{2}}} \\ & =-8.23\times {{10}^{-8}}\ \text{N} \\ \end{align}}\)

由於 \({{Q}_{p}}\) 為正、\({{Q}_{e}}\) 為負，所以 \({{F}_{coul}}\) 的計算結果是負數，表示靜電力是吸力。

氫原子中質子與電子間的靜電力

根據萬有引力定律，質子和電子之間的萬有引力 \({{F}_{grav}}\) 等於：

\(\displaystyle{{{F}_{grav}}=G\frac{{{m}_{p}}\ {{m}_{e}}}{{{r}^{2}}}}\)
\(\displaystyle{\begin{align} & =\left( 6.67\times {{10}^{-11}} \right)\frac{\left( 1.67\times {{10}^{-27}} \right)\left( 9.1\times {{10}^{-31}} \right)}{{{\left( 0.529\times {{10}^{-10}} \right)}^{2}}} \\ & =3.62\times {{10}^{-47}}\ \text{N} \\ \end{align}}\)

由於萬有引力定律中，質量（\({{m}_{p}}\) 和 \({{m}_{e}}\)）沒有正負之分，所以 \({{F}_{grav}}\) 必定是吸力。

由上方的計算結果，比較兩力的大小顯示：

\({{F}_{coul}}\) > \({{F}_{grav}}\)

氫原子中質子與電子間的萬有引力

【題解】
靜電力與萬有引力的比值為：

\(\begin{align*} \frac{{{F}_{coul}}}{{{F}_{grav}}} &= \frac{8.23\times {{10}^{-8}}}{3.62\times {{10}^{-47}}} \\ &= 2.27 \times 10^{39} \end{align*}\)

換言之，靜電力是萬有引力的 \(2.27 \times 10^{39}\) 倍。可見，電子與質子之間的靜電吸力比萬有引力大得多。