計算概率很多時需要點算滿足事件的可能結果數目,以及計算概率空間的大小;而組合數學就是點算中最為強大的工具。此兩者都是我們學過的,只需要多練習就可以把它們結合起來運用。我們會在這一節精研一個概率問題,同學可以在多項選擇題找到更多例子。
小珙與小鶯是長安城中的一對戀人。如圖所示,小珙住在永陽坊西南角;小鶯住在小珙以東 \(8\) 個街口,以北 \(6\) 個街口的永寧坊東北角。
這一天,小珙決定直接去小鶯家,一路只向東或向北走。
剛好城裏小販某甲這天在長壽坊東南角賣小鶯最愛吃的冰糖壺盧。長壽坊在小珙住處以東 \(2\) 個街口,以北 \(5\) 個街口。
小珙對某甲的行縱事前並無所知,且每條可能路線被挑中的機會是一樣的,請問他在路上遇到某甲的概率是多少?
(注意:故事内容純屬虛構)
根據概率定義,答案顯然是 $$\frac{\mbox{遇到某甲的路徑數目}}{\mbox{所有可能路徑數目}}。$$ 我們餘下的任務便是運用組合數學計算這兩個路徑數目。
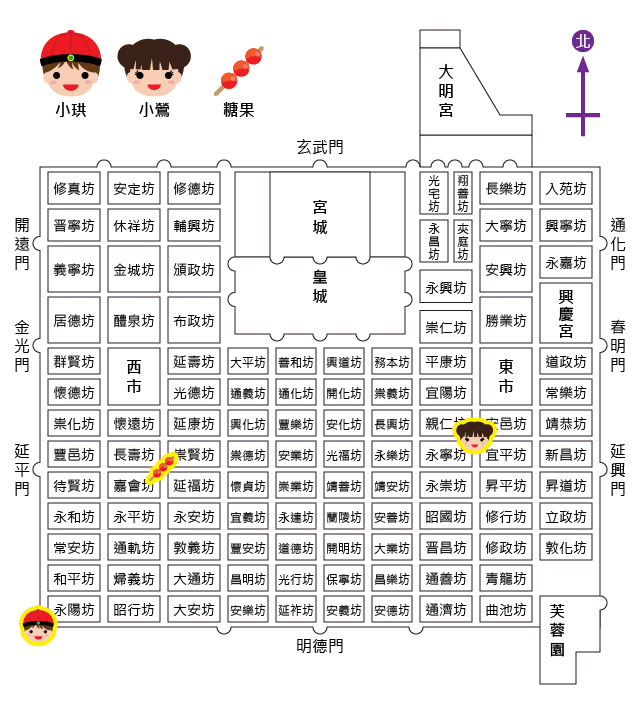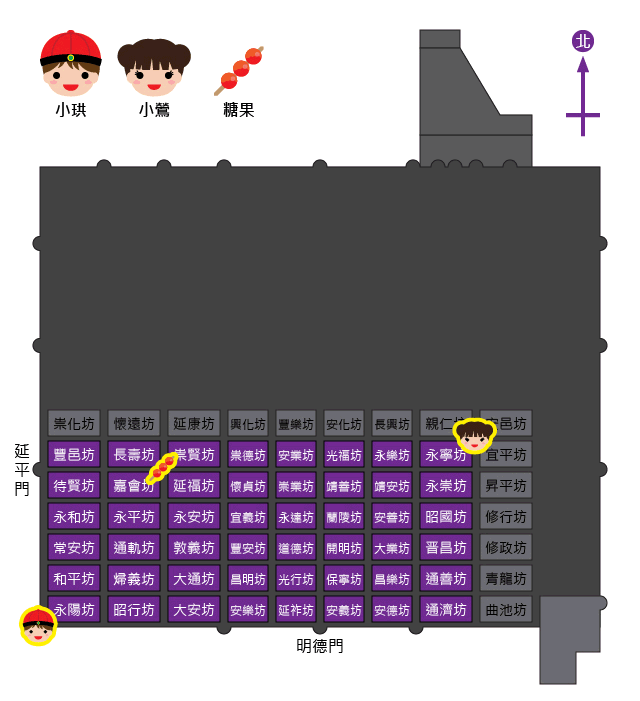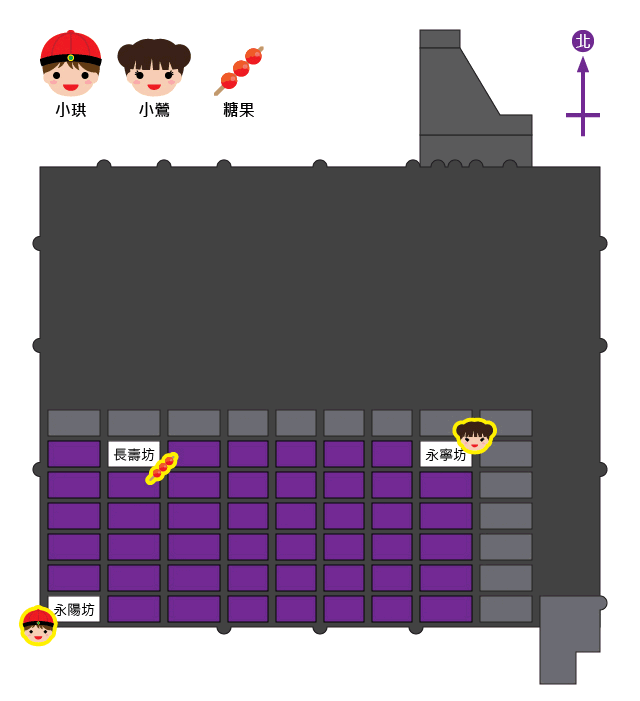
長安城示意圖
我們首先問自己一個關鍵問題:
假設小珙要走到離自己以東 \(m\) 個街口,以北 \(n\) 個街口,為了最快到達目的地,他只往東或北行走,則總共有多少種走法?
同學可以透過互動素材幫助思考。
\(\displaystyle C^{m+n}_n=\frac{(m+n)!}{m!n!}\)
\(m+n\)
\(mn\)
無法判斷
題解:
以→記錄小珙一個街口向東走到另一個街口,以↑記錄小珙一個街口向北走到另一個街口。紀錄便與路徑一一對應。
無論小珙如何走,只要他從不向西或南行,記錄長度必為 \(m+n\),路線中必有 \(m\) 個→ 和 \(n\) 個↑。
反之,\(m\) 個→ 和 \(n\) 個↑的任何排列組合都代表一個可能路徑。
所有可能路徑數目就是在長度為 \(m+n\) 的記錄中選取 \(m\) 個↑的組合數目,也就是 \(\displaystyle C^{m+n}_n=\frac{(m+n)!}{m!n!}\)。
回到我們的問題,現在我們已可以計算所有可能路徑數目為 \(\displaystyle C^{8+6}_6=\frac{14!}{8!\times 6!}=3003\) 條。
那麼路上遇到某甲的路徑數目又是多少?
同學可以透過互動素材幫助思考。
\(C^{2+5}_2=21\)
\(C^{6+1}_1=7\)
\(C^{2+5}_2 \times C^{6+1}_1 = 147\)
無法判斷
題解:
根據組合的數目,由出發點到小販某甲處有路徑 \( C^{2+5}_2=21\) 條;由某甲處到小鶯住處有路徑 \( C^{(8-2)+(6-5)}_{6-5} = C^{6+1}_1=7 \) 條。
根據組合數學的乘法法則,小珙直接去小鶯家路上遇到某甲的路徑有 \( 21\times 7 =147\) 條。
所以,小珙在前往小鶯家的路上遇到某甲的概率就是 $$\frac{\mbox{路上遇到某甲的路徑數目}}{\mbox{所有可能路徑數目}}=\frac{147}{3003}=\frac{7}{143}。$$ 一般而言,考慮小鶯住在小珙以東 \(m\) 個街口,以北 \(n\) 個街口;小販出現在小珙以東 \(0\leq i \leq m\) 個街口,以北 \(0\leq j\leq n\) 個街口。小珙決定直接去小鶯家,一路只向東或向北走,並對某甲的行縱事前一無所知,且每條可能路線被挑中的機會是一樣的。他在路上遇到某甲的概率就是 \[\displaystyle \frac{\mbox{路上遇到某甲的路徑數目}}{\mbox{所有可能路徑數目}}=\frac{C^{i+j}_j\times C^{m-i+n-j}_{n-j}}{C^{m+n}_n}。\]