這裡有兩個可能性：

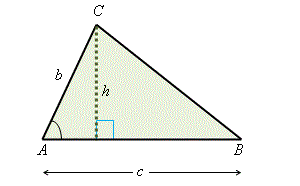
考慮\(\,\triangle ABC\)(\(\,\angle CAB\)是銳角)，

\[\begin{align} \sin A &= \frac{h}{b}\\ h &= b\sin A \end{align}\]

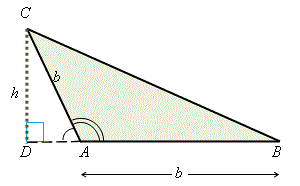
考慮\(\,\triangle ABC\)(\(\,\angle CAB\)是鈍角)，

\[\begin{align}\sin (180^\circ-A) &= \frac{h}{b}\\ h &= b\sin (180^\circ - A) = b \sin A \end{align}\]

在初中，我們學過三角形面積的公式是

面積\(\; \displaystyle = \frac{1}{2}\times\,\)高\(\,\times \,\)底

注意：

為何在以上的三角形面積公式中，所涉及的角必須是夾角。你知道為為甚麼嗎？

提示：

你能否找到這兩個三角形符合相同已知條件(兩邊的邊長及一個非夾角)的三角形，但它們的面積卻是不相同？