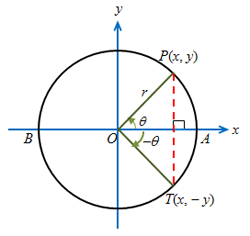
在右面的模擬模型中,圓的半徑為\(\,r \,\),圓心為原點,\(\,\triangle AOP = \theta \,\)。\(\,P(x, y)\,\)是圓上的一點。
i) 設\(\, T \,\)為圓上的一點,且負角\(\,\angle AOT = - \theta \,\)(見圖右)。
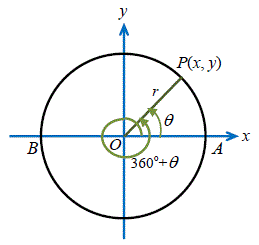
把\(\,P(x, y)\,\)點沿原點\(\,O \,\)旋數\(\,360^\circ\,\)可得同點\(\,P \,\)(見圖右)。
因此,對於任意一個銳角\(\,\theta \,\),
\begin{align*} \sin (-\theta)&=& \sin (360^\circ + \theta) &=& \sin \theta\\ \cos (-\theta)&=& \cos (360^\circ + \theta) &=& \cos \theta \\ \tan (-\theta)&=& \tan (360^\circ + \theta) &=& \tan \theta \end{align*}
考慮以下弦長\(\;1\;\)單位的三角形,
我們有
\begin{align*} \sin (90^\circ -\theta)&= \cos \theta ,\\ \cos (90^\circ -\theta)&= \sin \theta ,\\ \tan (90^\circ -\theta)&=\frac{\sin (90^\circ -\theta)}{\cos (90^\circ -\theta)}\\ &=\frac{\cos \theta}{\sin \theta}\\ &= \frac{1}{\tan \theta}。 \end{align*}設\(\,\phi = {90^\circ} + \theta \,\)。