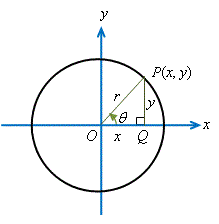在右圖中，設\(\,r>0 \,\)為圓的半徑。

考慮象限I中的直角三角形\(\,\triangle OPQ\,\)，\(P\,\)的座標為\(\,(x,y)\)，旋轉角\(\,\theta \,\)為銳角，則其三角比的定義如下：

例如：對於任意銳角\(\,\theta \,\)，

\begin{align*} \mathrm{正弦 }：& \sin \theta &= { \frac{對邊(PQ)}{斜邊(OP)}} &= { \frac{y}{r}} &= { \frac{y}{\sqrt{x^2+y^2}}}\\ \mathrm{餘弦 }：& \cos \theta &= { \frac{鄰邊(OQ)}{斜邊(OP)}} &= { \frac{x}{r}} &= { \frac{x}{\sqrt{x^2+y^2}}}\\ \mathrm{正切 }：& \tan \theta &= { \frac{對邊(PQ)}{鄰邊(OQ)}} &= { \frac{y}{x}} &\\ \end{align*}

其中\(\,x \ne 0\,\)。