在直角坐標平面上,整個平面被\(\,x\,\)軸和\(\,y\,\)軸平均地分為四個部份,每一個部份稱為一個象限(quadrant)。四個象限分別稱為象限 I、II、III和IV,如圖所示。
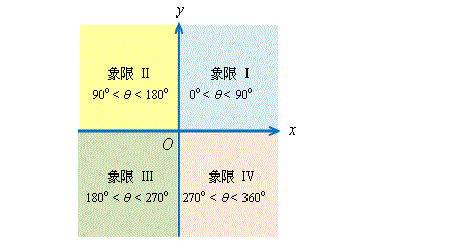
各象限內正旋轉角的取值範圍如下:
| 以度數為單位 | 以弧度為單位 | |
|---|---|---|
| 象限I | \(\,0^\circ< \theta < 90^\circ\,\) |
\(\,0 < \theta < \frac{\pi}{2}\,\) |
| 象限II | \(\,90^\circ< \theta < 180^\circ\,\) |
\(\,\frac{\pi}{2} < \theta < \pi\,\) |
| 象限III | \(\,180^\circ< \theta < 270^\circ\,\) |
\(\,\pi < \theta < \frac{3\pi}{2}\,\) |
象限IV |
\(\,270^\circ< \theta < 360^\circ\,\) |
\(\,\frac{3\pi}{2} < \theta < 2\pi\,\) |
請留意:坐標軸並不屬於任何一個象限。所以\(\,90^\circ \)、\(\,180^\circ\)、\(\,270^\circ\,\)及\(\,360^\circ\,\)等角不屬於任何一個象限。
再留意:以度數為單位的量度與以弧度為單位的量度成正比。