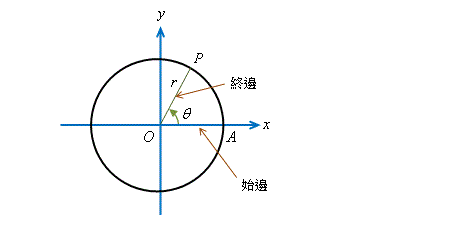
在直角坐標平面上,考慮一個以原點\(\,O\,\)為圓心、半徑為\(\,r\,\)的圓。
設\(\,A\,\)點為圓與正\(\,x\,\)軸的交點,即\(\,OA\,\)是一條在\(\,x\,\)軸上的線段。設\(\,P \,\)點為圓周上的任何一點。
我們有以下的定義:
| \(\,OA\,\) | 始邊 |
|---|---|
| \(\,OP\,\) | 終邊 |
\(\,\angle AOP \, (\theta )\,\) 依反時針方向 |
旋轉角 |
旋轉角可分為以下兩類:
依反時針方向旋轉\(\,\huge \curvearrowleft\,\)而成的為正角。在互動素材中,請移動數值滑桿來設\(\,\angle AOP = +120^\circ\,\)(或簡記作\(\,\angle AOP = 120^\circ\,\)),並觀察其圖像。
依順時針方向旋轉\(\,\huge \curvearrowright\,\)而成的為負角。在互動素材中,請移動數值滑桿來設\(\,\angle AOP = -40^\circ\,\),並觀察其圖像。