
二項式係數的特性等價於組合的特性。在基礎課程的這一課中,我們已列出了一些,並給了兩種證明。現在,我們用代數方法再證明一次。同學可以借此比較不同的思路,以發挖合適自己的思維模式。
| 特性 | 證明 |
|---|---|
|
對於整數\(\;0\leq r\leq n\),我們有以下等式 \begin{align*} C^n_r=C^n_{n-r} \end{align*} |
命題對於整數\(\;0\leq r\leq n\),我們有以下等式 \begin{align*} C^n_r=C^n_{n-r}。 \end{align*} 證明考慮以下代數運算 \begin{eqnarray*} &(1+x)^n&=&(x+1)^n\\ \Rightarrow & \sum_{i=0}^{n} C^n_{i} x^i &=& \sum_{i=0}^{n} C^n_i x^{n-i}\\ \Rightarrow & \sum_{r=0}^{n} C^n_{r} x^r &=& \sum_{r=0}^{n} C^n_{n-r} x^{r} \end{eqnarray*} 應用二項展式,我們得到上面的等式。 對於整數\(\;0\leq r\leq n\),比較上式左右兩邊\(\;x^r\;\)項的係數,即得 \begin{align*} C^n_r=C^n_{n-r}。 \end{align*} 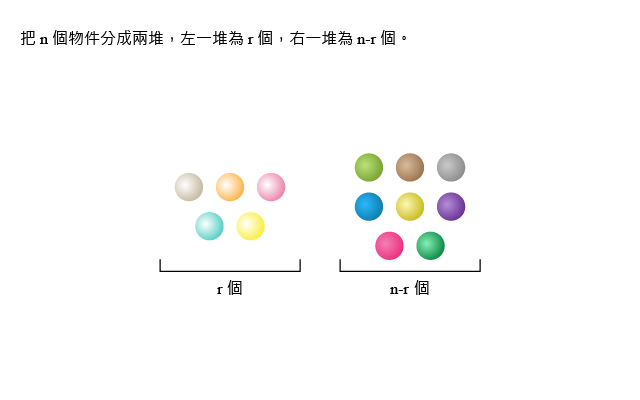
考慮\(\;n\;\)個相異物件。我們可以把它們分為左右兩堆,左邊一堆數目為\(\;r\;\)個,右邊一堆數目為\(\;n-r\;\)個。 從左邊那堆看,可能的分法有\(\;C^n_r\;\)種;從右邊那堆看,可能的分法有\(\;C^n_{n-r}\;\)種。 這兩種數法的答案必需是一致的,所以\(\;C^n_r=C^n_{n-r}\)。 \begin{align*} &C^n_r\\ =&\frac{n!}{r!(n-r)!}\\ =&\frac{n!}{(n-r)!(n-(n-r))!}\\ =&C^n_{n-r}。 \end{align*}
|
|
對於整數\(\;1\leq r\leq n-1\),我們有以下等式 \begin{align*} C^{n-1}_{r}+C^{n-1}_{r-1} = C^n_r \end{align*} |
命題對於整數\(\;1\leq r\leq n-1\),我們有以下等式 \[\;C^{n-1}_{r}+C^{n-1}_{r-1} = C^n_r。\;\] 證明考慮以下代數運算 \begin{eqnarray*} &(x+1)^n&=&(x+1)\times(x+1)^{n-1}=x(x+1)^{n-1}+(x+1)^{n-1}\\ \Rightarrow & \sum_{i=0}^{n} C^n_{i} x^i &=& x\sum_{i=0}^{n-1} C^{n-1}_{i} x^i+\sum_{i=0}^{n-1} C^{n-1}_{i} x^i\\ \Rightarrow & \sum_{i=0}^{n} C^n_{i} x^i &=& \sum_{i=1}^{n} C^{n-1}_{i-1} x^i+\sum_{i=0}^{n-1} C^{n-1}_{i} x^i\\ \Rightarrow & \sum_{i=0}^{n} C^n_{i} x^i &=& 1+\left(\sum_{i=1}^{n-1} (C^{n-1}_{i-1}+C^{n-1}_{i}) x^i\right)+x^n \end{eqnarray*} 應用二項展式,我們得到上面的等式。 對於整數\(\;1\leq r\leq n-1\),比較上式左右兩邊\(\;x^r\;\)項的係數,即得 \begin{align*} C^n_r=C^{n-1}_{r-1}+C^{n-1}_{r}。 \end{align*} 對於\(\;n\;\)個相異物件,標記為\(\;1\;\)號、\(2\;\)號、\(\cdots\)、\(n\;\)號。我們從中選取\(\;r\;\)個物件的組合數目是\(\;C^n_r\)。 再考慮另一種數法:選取\(\;r\;\)個物件有兩類情況,選到\(\;n\;\)號和沒選到\(\;n\;\)號。 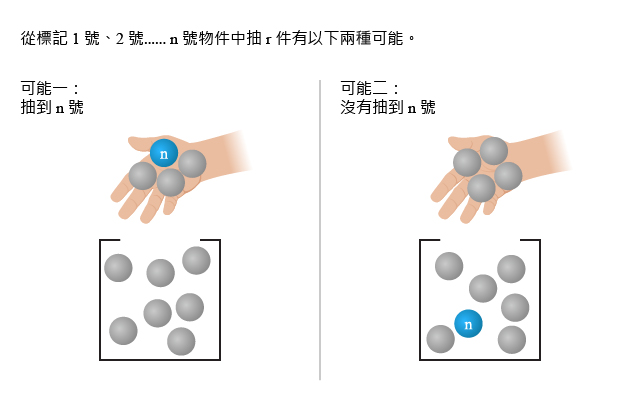
選到\(\;n\;\)號的組合數目,等於在標記為\(\;1\;\)號到\(\;n-1\;\)號的物件中,選取剩下\(\;r-1\;\)個物件的組合數目,也就是\(\;C^{n-1}_{r-1}\); 沒選到\(\;n\;\)號的組合數目,等於在標記為\(\;1\;\)號到\(\;n-1\;\)號的物件中,選取\(\;r\;\)個物件的組合數目,也就是\(\;C^{n-1}_{r}\)。 這兩種數法的答案必需是一致的,根據加法法則,\(C^{n-1}_{r}+C^{n-1}_{r-1} = C^n_r\)。 \begin{align*} &C^{n-1}_{r}+C^{n-1}_{r-1} \\ =&\frac{(n-1)!}{r!(n-r-1)!}+\frac{(n-1)!}{(r-1)!(n-r)!}\\ =&\frac{(n-r)\times (n-1)!}{r!(n-r)!}+\frac{r\times (n-1)!}{r!(n-r)!}\\ =&\frac{((n-r)+r)\times (n-1)!}{r!(n-r)!}\\ =&\frac{n!}{r!(n-r)!}\\ =&C^n_r。 \end{align*} |
|
對於整數\(\;1\leq r\leq n\),我們有以下等式 \begin{align*} C^{n-1}_{r-1}+C^{n-2}_{r-1}+\cdots+C^{r}_{r-1}+C^{r-1}_{r-1} =C^n_r \end{align*} |
命題對於整數\(\;1\leq r\leq n\),我們有以下等式 \begin{align*} C^{n-1}_{r-1}+C^{n-2}_{r-1}+\cdots+C^{r}_{r-1}+C^{r-1}_{r-1} =C^n_r \end{align*} 使用\(\;\sum\;\)記法,就是 \begin{align*} \sum_{i=r-1}^{n-1} C^{i}_{r-1}=C^n_r。 \end{align*}證明考慮以下代數運算 \begin{eqnarray*} &(x+1)^n &=&x(x+1)^{n-1}+(x+1)^{n-1}\\ & &=&x^2(x+1)^{n-2}+x(x+1)^{n-2}+(x+1)^{n-1}\\ & &\vdots&\\ & &=&x^{n}+x^{n-1}+x^{n-2}(x+1)+x^{n-3}(x+1)^{2}+\cdots+x(x+1)^{n-2}+(x+1)^{n-1}\\ %%\Rightarrow & &=&x^{n}+x^{n-1}+x^{n-1}(1+\frac{1}{x})+x^{n-1}(1+\frac{1}{x})^2+\cdots+x^{n-1}(1+\frac{1}{x})^{n-2}+x^{n-1}(1+\frac{1}{x})^{n-1}\\ & &=&x^{n}+\sum_{i=0}^{n-1} x^{n-1-i}(x+1)^i\\ & &=&x^{n}+x^{n-1}\sum_{i=0}^{n-1} (1+\frac{1}{x})^i\\ \Rightarrow & \sum_{i=0}^{n} C^n_{n-i} x^i &=&x^{n}+x^{n-1}\sum_{i=0}^{n-1} \sum_{j=0}^{i} \left( C^i_{j} \frac{1}{x^j} \right)\\ %\Rightarrow & \sum_{i=0}^{n} C^n_{n-i} x^i &=&x^{n}+x^{n-1}\sum_{0\leq j \leq i\leq n-1} \frac{C^{i}_{j}}{x^{j}} \\ \Rightarrow & \sum_{i=0}^{n} C^n_{n-i} x^i &=&x^{n}+x^{n-1}\sum_{j=0}^{n-1} \left( \frac{1}{x^{j}} \sum_{i=j}^{n-1} C^{i}_{j}\right) \end{eqnarray*} 應用二項展式,我們得到上面的等式。 對於整數\(\;1\leq r\leq n\),比較上式左右兩邊\(\;x^{n-r}\;\)項的係數,即得 \begin{align*} C^n_r=\sum_{i=r-1}^{n-1} C^{i}_{r-1}。 \end{align*} 對於\(\;n\;\)個相異物件,標記為\(\;1\;\)號、\(2\;\)號、\(\cdots\)、\(n\;\)號。我們從中選取\(\;r\;\)個物件的組合數目是\(\;C^n_r\)。 再考慮另一種數法:\(\;r\;\)個物件的組合中,標記最大的肯定不小於\(\;r\;\)號,於是選取\(\;r\;\)個物件有以下\(\;n-r+1\;\)類情況: 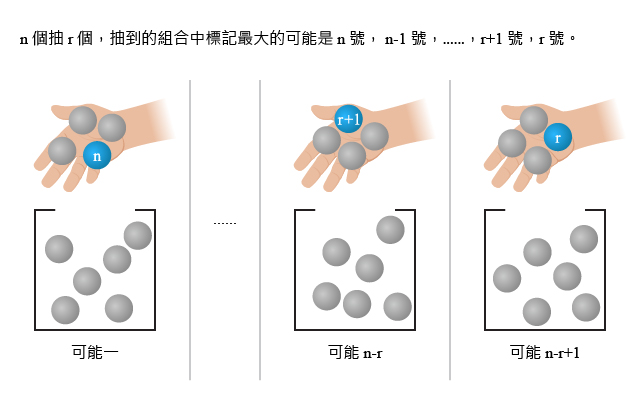
第一類,選到的組合中標記最大的為\(\;n\;\)號,則在標記為\(\;1\;\)號到\(\;n-1\;\)號的物件中,需要選取剩下\(\;r-1\;\)個物件,有\(\;C^{n-1}_{r-1}\;\)不同組合; 第二類,選到的組合中標記最大的為\(\;n-1\;\)號,則在標記為\(\;1\;\)號到\(\;n-2\;\)號的物件中,需要選取剩下\(\;r-1\;\)個物件,有\(\;C^{n-2}_{r-1}\;\)不同組合; \(\;\vdots\:\;\) 第\(\;n-r\;\)類,選到的組合中標記最大的為\(\;r+1\;\)號,則在標記為\(\;1\;\)號到\(\;r\;\)號的物件中,需要選取剩下\(\;r-1\;\)個物件,有\(\;C^{r}_{r-1}\;\)不同組合; 第\(\;n-r+1\;\)類,選到的組合中標記最大的為\(\;r\;\)號,則在標記為\(\;1\;\)號到\(\;r-1\;\)號的物件中,需要選取剩下\(\;r-1\;\)個物件,有\(\;C^{r-1}_{r-1}\;\)不同組合。 這兩種數法的答案必需是一致的,根據加法法則,\(C^{n-1}_{r-1}+C^{n-2}_{r-1}+\cdots+C^{r}_{r-1}+C^{r-1}_{r-1} =C^n_r\)。 \begin{align*} &C^{n-1}_{r-1}+C^{n-2}_{r-1}+\cdots+C^{r+1}_{r-1}+C^{r}_{r-1}+C^{r-1}_{r-1}\\ = &C^{n-1}_{r-1}+C^{n-2}_{r-1}+\cdots+C^{r+1}_{r-1}+C^{r}_{r-1}+C^{r}_{r}\\ = &C^{n-1}_{r-1}+C^{n-2}_{r-1}+\cdots+C^{r+1}_{r-1}+C^{r+1}_{r}\\ = &C^{n-1}_{r-1}+C^{n-2}_{r-1}+\cdots+C^{r+2}_{r-1}+C^{r+2}_{r}\\ = &C^{n-1}_{r-1}+C^{n-2}_{r-1}+\cdots+C^{r+3}_{r-1}+C^{r+3}_{r}\\ &\vdots\\ = &C^{n-1}_{r-1}+C^{n-2}_{r-1}+C^{n-3}_{r-1}+C^{n-3}_{r}\\ = &C^{n-1}_{r-1}+C^{n-2}_{r-1}+C^{n-2}_{r}\\ = &C^{n-1}_{r-1}+C^{n-1}_{r}\\ = &C^{n}_{r}。 \end{align*} |
|
對於整數\(\;m\geq 1\),我們有以下等式 \begin{align*} C^m_0+C^m_1+\cdots+C^m_{m-1}+C^m_m=2^m \end{align*} |
命題對於整數\(\;m\geq 1\),我們有以下等式 \[\;C^m_0+C^m_1+\cdots+C^m_{m-1}+C^m_m=2^m。\;\] 使用\(\;\sum\;\)記法,就是 \begin{align*} \sum_{i=0}^{m} C^m_i=2^m。 \end{align*}證明考慮二項展式 \begin{eqnarray*} (x+1)^m=\sum_{i=0}^m C^m_i x^i。 \end{eqnarray*} 在上面的等式代入\(\;x=1\),即得 \begin{eqnarray*} 2^m=(1+1)^m=\sum_{i=0}^m C^m_i 1^i=\sum_{i=0}^m C^m_i。 \end{eqnarray*} 我們考慮這個問題:在一堆為數\(\;m\;\)個的相異物件中隨手抓一把,有多少不同的結果? 一種數法是考慮每個物件都有兩種結果:被抓到或沒被抓到。 根據乘法法則,隨手抓一把的結果數目為\(\;2\times 2\times \cdots \times 2 = 2^m\;\)。 再考慮另一種數法,隨手抓一把有\(\;m+1\;\)類情況: 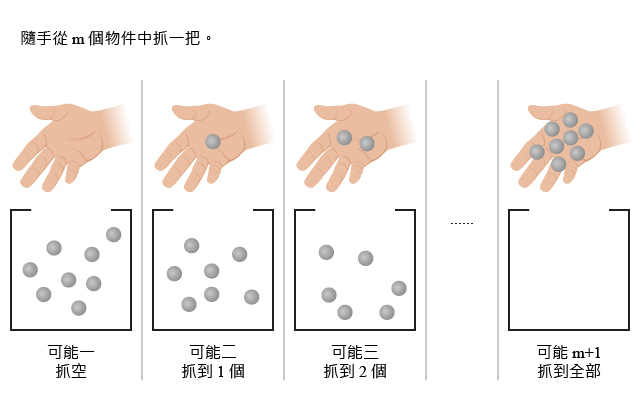
第一類,抓到\(\;0\;\)個物件,有\(\;C^{m}_{0}\;\)種不同結果; 第二類,抓到\(\;1\;\)個物件,有\(\;C^{m}_{1}\;\)種不同結果; \(\;\vdots\:\;\) 第\(\;m\;\)類,抓到\(\;m-1\;\)個物件,有\(\;C^{m}_{m-1}\;\)種不同結果; 第\(\;m+1\;\)類,抓到全部\(\;m\;\)個物件,有\(\;C^{m}_{m}\;\)種不同結果。 這兩種數法的答案必需是一致的,根據加法法則,\(C^m_0+C^m_1+\cdots+C^m_{m-1}+C^m_m=2^m \)。 \begin{align*} &C^m_0+C^m_1+C^m_2+\cdots+C^m_{m-2}+C^m_{m-1}+C^m_m \\ = &(C^{m-1}_0)+(C^{m-1}_0+C^{m-1}_1)+(C^{m-1}_1+C^{m-1}_2)+\cdots+(C^{m-1}_{m-2}+C^{m-1}_{m-1})+(C^{m-1}_{m-1})\\ = &2\times(C^{m-1}_0+C^{m-1}_1+C^{m-1}_2+\cdots+C^{m-1}_{m-3}+C^{m-1}_{m-2}+C^{m-1}_{m-1} )\\ = &2\times(2\times(C^{m-2}_0+C^{m-2}_1+C^{m-2}_2+\cdots+C^{m-2}_{m-4}+C^{m-2}_{m-4}+C^{m-2}_{m-2}))\\ = &2^2\times(C^{m-2}_0+C^{m-2}_1+C^{m-2}_2+\cdots+C^{m-2}_{m-4}+C^{m-2}_{m-4}+C^{m-2}_{m-2})\\ &\vdots\\ = &2^{m-1}\times (C^1_0+C^1_1)\\ = &2^{m-1}\times (1+1)\\ = &2^{m}。 \end{align*} |
|
對於整數\(\;m> 1\),我們有以下等式 \begin{align*} C^m_0+(-1)C^m_1+(-1)^2C^m_2+\cdots+(-1)^{m-1}C^m_{m-1}+(-1)^mC^m_m=0 \end{align*} |
重溫算術證明:命題對於整數\(\;m\geq 1\),我們有以下等式 \[\;C^m_0+(-1)C^m_1+(-1)^2C^m_2+\cdots+(-1)^{m-1}C^m_{m-1}+(-1)^mC^m_m=0 。\;\] 使用\(\;\sum\;\)記法,就是 \begin{align*} \sum_{i=0}^{m} (-1)^i C^m_i=0。 \end{align*}證明考慮二項展式 \begin{eqnarray*} (x+1)^m=\sum_{i=0}^m C^m_i x^i。 \end{eqnarray*} 在上面的等式代入\(\;x=-1\),即得 \begin{eqnarray*} 0=((-1)+1)^m=\sum_{i=0}^m (-1)^i C^m_i。 \end{eqnarray*} 我們考慮這個問題:在一堆為數\(\;m\;\)個的相異物件中隨手抓一把,抓到單數的結果與抓到雙數的結果一樣多嗎? 不妨先把物件標記為\(\;1\;\)號、\(2\;\)號、\(\cdots\)、\(m\;\)號。 在堆中隨手抓一把,結果可以分為以下四類: 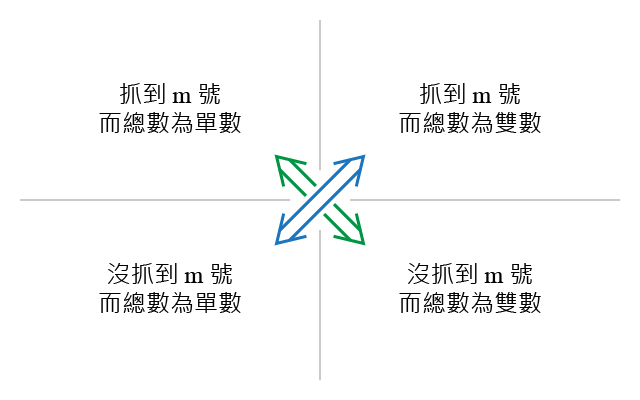
第一類,抓到\(\;m\;\)號而抓到的總數為單數; 第二類,抓到\(\;m\;\)號而抓到的總數為雙數; 第三類,沒抓到\(\;m\;\)號而抓到的總數為單數; 第四類,沒抓到\(\;m\;\)號而抓到的總數為雙數。 如果結果為第一類,去掉\(\;m\;\)號物件,結果就變為第四類;反之,如果結果為第四類,再抓上\(\;m\;\)號物件,結果就變為第一類。所以,第一類的結果與第四類的一樣多。 同樣地,第二類的結果又與第三類的一樣多。(如果結果為第二類,去掉\(\;m\;\)號物件,結果就變為第三類;反之,如果結果為第三類,再抓上\(\;m\;\)號物件,結果就變為第二類。所以,第二類的結果與第三類的一樣多。) 於是, \begin{align*} &\;|總數為單數的結果| \\ = &\;第一類加第三類的和 \\ = &\;第四類加第三類的和 \\ = &\;第四類加第二類的和 \\ = &\;|總數為雙數的結果| \end{align*} 所以雙數結果的數目減去抓到單數結果的數目為零,也就是說 \[C^m_0+(-1)C^m_1+(-1)^2C^m_2+\cdots+(-1)^{m-1}C^m_{m-1}+(-1)^mC^m_m=0。 \] \begin{align*} &C^m_0+(-1)C^m_1+(-1)^2C^m_2+\cdots+(-1)^{m-2}C^m_{m-2}+(-1)^{m-1}C^m_{m-1}+(-1)^mC^m_m\\ = &(C^{m-1}_0)-(C^{m-1}_0+C^{m-1}_1)+\cdots+(-1)^{m-2}(C^{m-1}_{m-2}+(-1)^{m-1}C^{m-1}_{m-1})+(-1)^{m}(C^{m-1}_{m-1})\\ = &(1+(-1))\times(C^{m-1}_0-C^{m-1}_1+C^{m-1}_2+\cdots+(-1)^{m-3}C^{m-1}_{m-3}+(-1)^{m-2}C^{m-1}_{m-2}+(-1)^{m-1}C^{m-1}_{m-1} )\\ = &0。 \end{align*} |
