我們已經學過計數原理的兩種基本法則:加法法則和乘法法則。
你知道在甚麼情況下應用哪一種法則嗎?
在本節,我們會練習如何綜合應用這兩種法則來解決較複雜的問題。
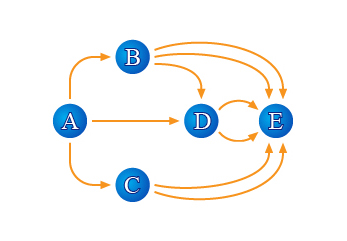
\(\;A\)、\(B\)、\(C\)、\(D\)、\(E\;\)五地之間有眾多免費單程巴士服務,如下圖所示。 透過配搭不同服務,你可以從\(\;A\;\)地免費到達\(\;E\;\)地;
其中經過\(\;D\;\)地的有 種配搭;
題解:
從\(\;A\;\)地免費到達\(\;D\;\)地有\(\;2\;\)個選擇(分別為經過\(\;B\;\)和不經過\(\;B\;\));從\(\;D\;\)地免費到達\(\;E\;\)地又有\(\;2\;\)個選擇;根據乘法法則,從\(\;A\;\)地經過\(\;D\;\)地免費到達\(\;E\;\)地有\(\;2\times2=4\;\)種選擇。
從\(\;A\;\)地不經過\(\;D\;\)地有\(\;2\;\)個直接目的地,分別為\(\;B\;\)和\(\;C\);\(B\;\)和\(\;C\;\)各有\(\;2\;\)個選擇不經過\(\;D\;\)地免費到達\(\;E\;\)地又有;根據乘法法則,從\(\;A\;\)地不經過\(\;D\;\)地免費到達\(\;E\;\)地有\(\;2\times2=4\;\)種選擇。
從\(\;A\;\)地免費到達\(\;E\;\)地的路線有兩種:經過\(\;D\;\)地和不經過\(\;D\;\)地;則根據加法法則,從\(\;A\;\)地免費到達\(\;E\;\)地共有\(\;4+4=8\;\)種配搭。
小饕想做一個漢堡包,需要配撘一種芝士和一種肉扒。他家中有\(\;3\;\)款芝士,\(2\;\)款牛扒,\(1\;\)款羊扒,\(1\;\)款雞扒,則他做的漢堡包有多少種可能的配搭呢?
配搭有兩個步驟:
第一步選芝士,有\(\;3\;\)種;
第二步選肉扒,有牛扒、羊扒、雞扒,根據加法法則,共有\(\;2+1+1=4\;\)種。
則根據乘法法則,所有配搭共有\(\;3\times 4=12\;\)種配搭。
.png)
考慮甲班\(\;5\;\)男\(\;8\;\)女和乙班\(\;6\;\)男\(\;4\;\)女的兩個班別, 在一場聯班舞會中老師要挑選一男一女到台上表演。如果限定這兩人來自不同班別,可能的配搭就有多少種?
配搭有兩類:
第一類甲班挑選一男,乙班挑選一女,則根據乘法法則,這類有配搭有\(\;5\times4=20\;\)種;
第二類乙班挑選一男,甲班挑選一女,則根據乘法法則,這類有配搭有\(\;6\times8=48\;\)種。
則根據加法法則,所有配搭共有\(\;20+48=68\;\)種。
如果撤銷限制,可能的配搭又有多少種?
第一步挑選一男,男生有兩類:甲班的男生和乙班的男生,根據加法法則,男生共有\(\;5+6=11\;\)個;
第二步挑選一女,女生有兩類:甲班的女生和乙女的男生,根據加法法則,女生共有\(\;4+8=12\;\)個;
則根據乘法法則,撤銷限制後,所有配搭共有\(\;11\times 12=132\;\)種。

如互動素材所示,\(A_1A_2A_3A_4A_5A_6A_7A_8A_9A_{10}A_{11}\;\)是一個正十一邊形,在十一個頂點上任意選三點可以構作一個三角形,請問三角形總共有多少個?
我們先數一數有多少個三角形和該三角形上的一個頂點與其配對。考慮兩個做法:
做法一可以分為兩步,先選三點構作一個三角形,然後在三角形上選一點;
做法二也可以分為兩步,先選一點,然後再構作一個包含該點的三角形;
這兩種做法得到的配對數目必然是一樣的,則根據乘法法則,
\begin{align*} & \mbox{任意三角形數目}\times 3=11 \times\mbox{包含一特定點的三角形數目}\\ \Rightarrow & \mbox{任意三角形數目}=\frac{11}{3}\times \mbox{包含一特定點的三角形數目}。 \end{align*}
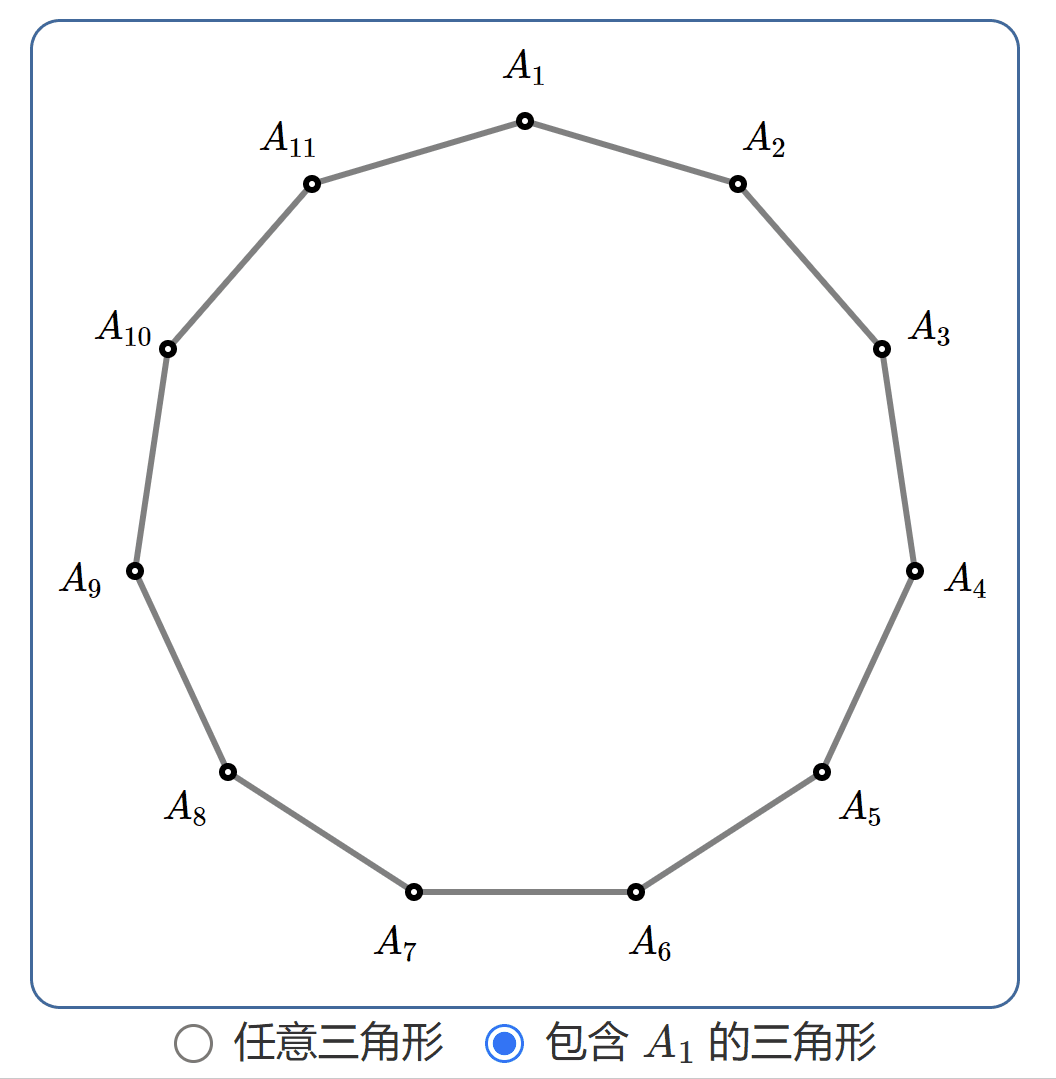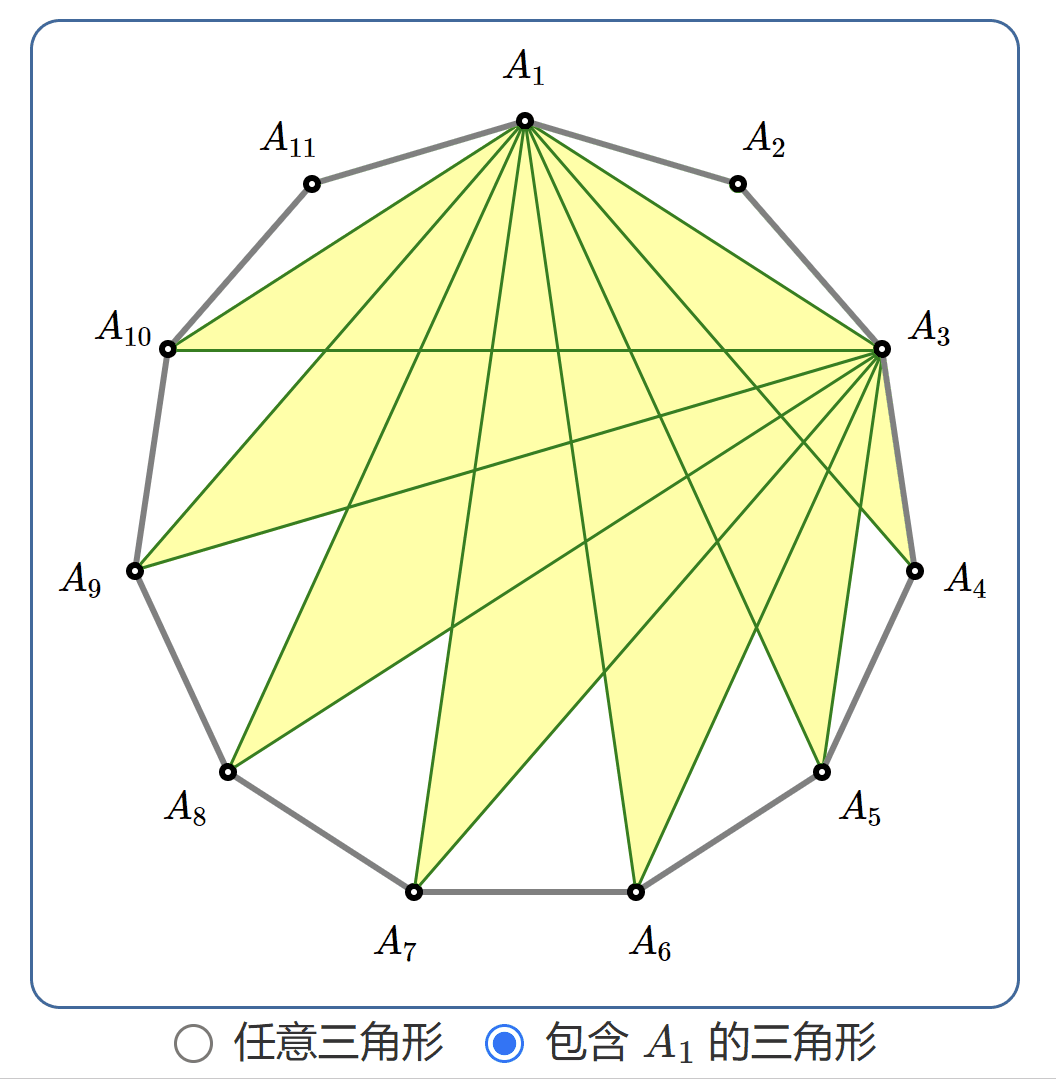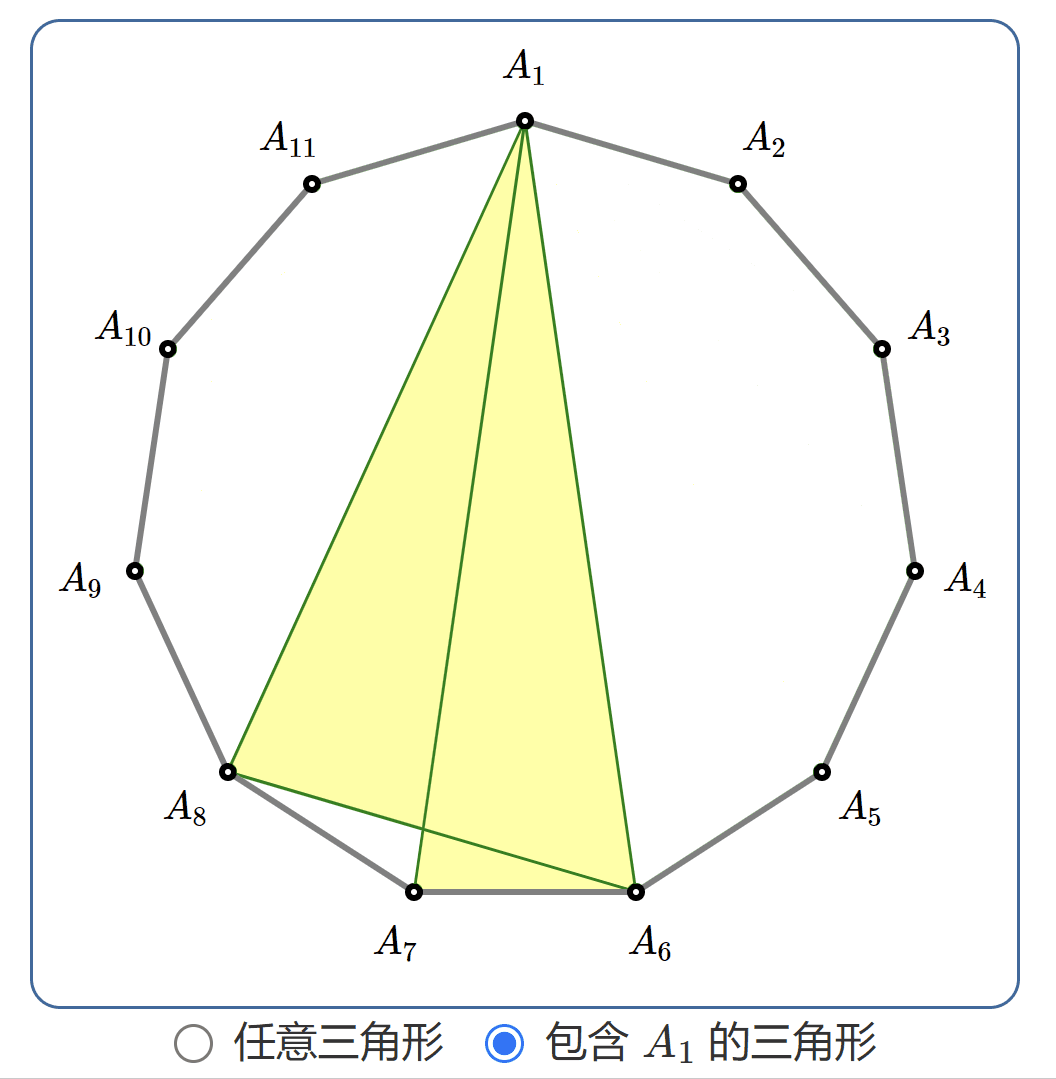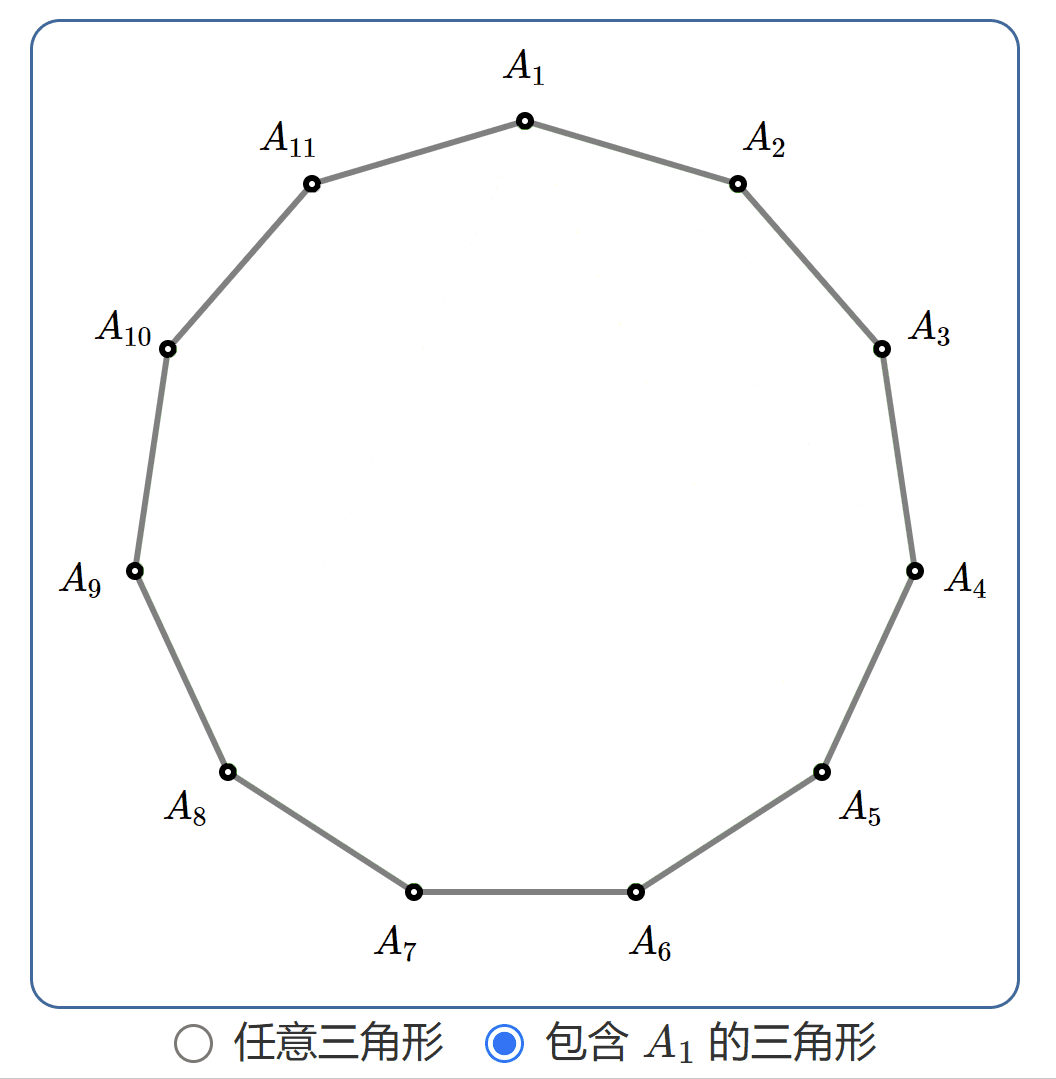
不妨假設特定點為\(\;A_1\),現在我們只需要數一下包含\(\;A_1\;\)的三角形數目。如圖所示,這樣的三角形可以按照\(\;A_1\;\)順時針下一個頂點分為九類:
第一類\(\;A_1\;\)順時針下一個的頂點為\(\;A_2\),有\(\;9\;\)個;
第二類\(\;A_1\;\)順時針下一個頂點為\(\;A_3\),有\(\;8\;\)個;
\(\;\vdots\;\)
第八類\(\;A_1\;\)順時針下一個頂點為\(\;A_9\),有\(\;2\;\)個;
第九類\(\;A_1\;\)順時針下一個頂點為\(\;A_{10}\),有\(\;1\;\)個;
則根據加法法則包含\(\;A_1\;\)的三角形有\(\;9+8+\cdots+2+1=\frac{10\times 9}{2}=45\;\)個。
根據上面的討論,任意三角形數目\(\;=\frac{11}{3}\times 45=165\;\)個。