在上一課的學習中,我們注意到:聯變只涉及到變量的乘法或除法運算。細心的同學可能會問,如果變量間還有加法或減法運算,那麼會是怎麼樣的一種變分關係呢?
這種關係是部分變,也是這一課大家將要學習的內容。相信大家學完之後,可以發現生活中,其實有很多的部分變的例子。
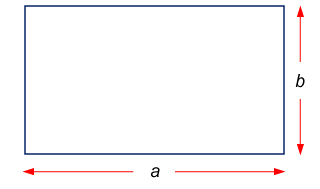
對於一個長度是\(\;a\;\)而闊度是\(\;b\;\)的長方形,它的周界\(\;P\;\)可以用以下方程表示:
\[P=2a+2b\]
我們也可以說,長方形的周界部分隨其長度正變,另一部分隨其闊度正變闊。
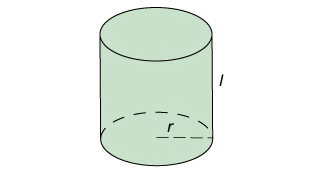
對於一個底面半徑是\(\;r\;\)而高是\(\;l\;\)的圓柱,它的總表面積\(\;A\;\)可以用以下方程表示:
\[A=2\pi r^2+2\pi rl\]
我們也可以說,圓柱的總表面積部分隨其底面半徑的平方正變,另一部分隨其底面半徑及其高聯變。
志榮在一家地產公司做經紀。他的月薪由兩部分組成:第一部分是固定的底薪\(\;5000\;\)元,第二部分將根據他的銷售業績按百分之\(\;5\;\)提成。
假設志榮在某個月的銷售總額為\(\;M\;\)元,其月薪為\(\;W\;\)元可以用以下方程表示:
\[W=\frac{M}{20} + 5000\]
我們也可以說,志榮的月薪部分隨他的銷售總額正變,另一部分是個常數。

某主題公園的“一日門票”按如下規則收費:
| 門票類別 | 門票價格(元) |
|---|---|
| 成人 | \(\;350\;\) |
| 小童 | \(\;250\;\) |
某旅行社考慮組團參觀該主題公園。
假設旅行團全部由成人和小童組成,其中成人有\(\;n\;\)人,小童有\(\;m\;\)人。該旅行團應支付門票的總開支為\(\;S\;\)元。\(S\;\)可以用以下方程表示:
\[S=350n+250m\]
我們也可以說,門票的總開支部分隨成人團員正變,另一部分隨小童團員正變。

一個變量由不同部分組成,每個部分可能是常數,也可能隨一些變量聯變。下表列出一些常見的部分變和對應的方程:
| 方程 | 圖像 |
|---|---|
| \(\;p\;\)部分是定量,部分隨\(\;x\;\)而正變。則 \[p=k_1+k_2x,\]其中\(\;k_1\;\)和\(\;k_2\;\)為常數\(\;(k_2\neq 0)\)。 |
|
| \(\;q\;\)部分隨\(\;x\;\)而正變,部分隨\(\;x^2\;\)而反變。則 \[q=k_3x+\frac{k_4}{x^2},\]其中\(\;k_3\;\)和\(\;k_4\;\)為常數\(\;(k_4\neq 0)\)。 |
|
| \(\;r\;\)部分隨\(\;x\;\)而正變,部分隨\(\;y\;\)而反變。則 \[r=k_5x+\frac{k_6}{y},\]其中\(\;k_5\;\)和\(\;k_6\;\)為常數\(\;(k_5, k_6 \neq 0)\)。 | 這個部分變關係涉及\(\;3\;\)個變量,其圖像是三維空間中的一個曲面。 |