在前面的模組,我們已學過兩個變量間最常見的關係:一個變量隨另一變量正變或反變。現實的情況往往更為複雜,一個變量可以同時受多個變量影響,隨著某些變量正變,又隨著另一些變量反變。同時考慮這些變量,能讓我們的計算更為精準。

在上一課我們有湊錢買壽桃的例子:一眾小孫子打算湊錢,買一個原價\(\;36288\;\)元的壽桃給爺爺祝壽,當中人均分擔費用就隨湊錢人數反變。
鑑於近日金價下跌,店家決定把壽桃打折扣優惠,則人均分擔費用同時亦隨著店家的折扣正變:
\[\mbox{人均分擔費用}=\frac{36288}{\mbox{湊錢人數}}\times \mbox{折扣優惠}。\]
同學可能透過互動素材,查看湊錢人數與折扣優惠對應的人均費用。
變量的定義域不一定是整條實數線。在這例子中就湊錢人數只包括從\(\;1\;\)到\(\;12\;\)的整數;店家折扣則不低於\(\;5\;\)折。
一個變量\(\;T\;\)正變於變量\(\;x_1,x_2,\cdots,x_m\),又反變於非零變量\(\;y_1,y_2,\cdots,y_n\),當中\(\;x_1,x_2,\cdots,x_m,y_1,y_2,\cdots,y_n\;\)並無關係。 我們便寫
\[T\propto \frac{x_1x_2\cdots x_m}{y_1 y_2 \cdots y_n};\]
也可以引入非零常數\(\;k\;\)並寫
\[T=k\frac{x_1x_2\cdots x_m}{y_1 y_2 \cdots y_n}。\]
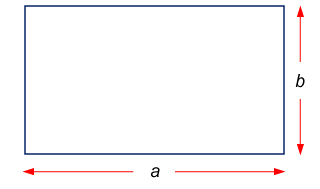
對於一個長度是\(\;a\;\)而闊度是\(\;b\;\)的長方形,它的面積\(\;S\;\)可以用以下方程表示:
\[S=ab\]
我們可以說,長方形的面積隨其長度正變,同時又隨其闊度正變。
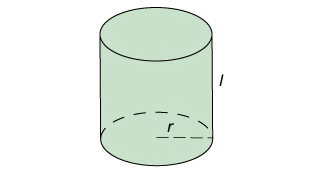
對於一個底面半徑是\(\;r\;\)而高是\(\;l\;\)的圓柱,它的體積\(\;V\;\)可以用以下方程表示:
\[V=\pi r^2 l\]
我們可以說,圓柱的體積隨其底面半徑的平方正變,同時又隨其高正變。
某地年利率為\(\;r\%\),小敏希望在一年後賺取利息\(\;I\;\)元,則她需要把存入的款項\(\;P\;\)可以用以下方程計算:
\[P=\frac{100I}{r}\]
我們可以說,\(\;P\;\)隨\(\;I\;\)正變又隨\(\;r\;\)反變。

在物理世界中,聯變也是十分常見。同學可以參考物理的課件。