二次函數常常表示成以下的形式:
一般式:\(\displaystyle{y=a{{x}^{2}}+bx+c\left( a\ne 0 \right) }\)
頂點式: \(\displaystyle{y=a{{\left( x-h \right)}^{2}}+k\left( a\ne 0 \right) }\)
交點式:\(\displaystyle{y=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)\left( a\ne 0 \right) }\)
其中,\(\displaystyle{a }\)、\(\displaystyle{b }\)、\(\displaystyle{ c}\)、\(\displaystyle{ h }\)、\(\displaystyle{ k }\)、\(\displaystyle{{{x}_{1}} }\) 和 \(\displaystyle{{{x}_{2}} }\) 都是常數。
思考:三種二次函數的形式是否可以相互轉化呢?
(1) 頂點式和交點式通過展開括弧可以轉化為一般式:
頂點式:\(\displaystyle{y=a{{\left( x-h \right)}^{2}}+k}\) \(\displaystyle{=a{{x}^{2}}-2ahx+\left( a{{h}^{2}}+k \right)\left( a\ne 0 \right) }\)
交點式:\(\displaystyle{y=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right) }\) \(\displaystyle{=a{{x}^{2}}-a\left( {{x}_{1}}+{{x}_{2}} \right)x+a{{x}_{1}}{{x}_{2}}\left( a\ne 0 \right)}\)
(2) 一般式和交點式可以通過配方法轉化為頂點式:
一般式:\(\displaystyle{y=a{{x}^{2}}+bx+c }\) \(\displaystyle{=a{{\left( x+\frac{b}{2a} \right)}^{2}}+\frac{4ac-{{b}^{2}}}{4a}\left( a\ne 0 \right) }\)
交點式:\(\displaystyle{y=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right) }\)
\(\displaystyle{=a{{\left( x-\frac{{{x}_{1}}+{{x}_{2}}}{2} \right)}^{2}}-\frac{a{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}}{4}\left( a\ne 0 \right) }\)
(3) 當二次方程 \(\displaystyle{a{{x}^{2}}+bx+c=0\left( a\ne 0 \right) }\) 有實數解時,即 \(\displaystyle{{{b}^{2}}-4ac\ge 0 }\),一般式可以轉化為交點式:
一般式:\(\displaystyle{y=a{{x}^{2}}+bx+c }\)
\(\displaystyle{ =a\left( x-\frac{-b+\sqrt{{{b}^{2}}-4ac}}{2a} \right)\left( x-\frac{-b-\sqrt{{{b}^{2}}-4ac}}{2a} \right)\left( a\ne 0 \right) }\)
當二次方程 \(\displaystyle{a{{\left( x-h \right)}^{2}}+k=0\left( a\ne 0 \right) }\) 有實數解時,即 \(\displaystyle{a\cdot k\le 0 }\),頂點式可以轉化為交點式:
頂點式:\(\displaystyle{y=a{{\left( x-h \right)}^{2}}+k }\)
\(\displaystyle{=a\left[ x-\left( h+\sqrt{-\frac{k}{a}} \right) \right]\cdot \left[ x-\left( h-\sqrt{-\frac{k}{a}} \right) \right]\left( a\ne 0 \right) }\)
根據上一節的學習內容,我們知道二次函數 (quadratic function) \(\displaystyle{y=a{{x}^{2}}+bx+c }\) 的圖像是一條拋物線 (parabola)。除形狀之外,我們透過以下的數學實驗來探索二次函數圖像的其他特徵。
該實驗提供了二次函數的三種表達形式,分別是:一般式 \(\displaystyle{y=a{{x}^{2}}+bx+c }\)、頂點式 \(\displaystyle{y=a{{\left( x-h \right)}^{2}}+k}\) 和交點式 \(\displaystyle{y=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)}\)。選定二次函數的某種表達形式後,改變其相應的參數,觀察函數圖像的特徵有何變化。通過上下移動水平線的位置,改變水平線與二次函數圖像的交點,考察二次函數的對稱性。
實驗圖像中,點 \(\displaystyle{ A }\) 是二次函數的頂點,點 \(\displaystyle{ B }\) 是函數圖像與 \(\displaystyle{ y }\) 軸的交點,\(\displaystyle{ C }\)、\(\displaystyle{ D }\) 兩點是函數圖像與 \(\displaystyle{ x }\) 軸的交點,\(\displaystyle{ P }\)、\(\displaystyle{ Q }\) 兩點是圖像與水平線的交點,點 \(\displaystyle{ O }\) 為水平線與穿過點 \(\displaystyle{ A }\) 的鉛垂線的交點。
觀察1:二次函數圖像的開口方向
「∪」 表示開口向上,「∩」 表示開口向下。
(1) 當 \(\displaystyle{ a \gt 0 }\) 時,二次函數圖像的開口:
(2) 當 \(\displaystyle{ a \lt 0 }\) 時,二次函數圖像的開口:
(3) 當 \(\displaystyle{ a \gt 0 }\) 時,隨著 \(\displaystyle{ a }\) 值的增大,二次函數圖像的開口大小:
(4) 當 \(\displaystyle{ a \lt 0 }\) 時,隨著 \(\displaystyle{ a }\) 值的增大,二次函數圖像的開口大小:
觀察2:二次函數的頂點和對稱性
(1) 當 \(\displaystyle{ a \gt 0 }\) 時,二次函數圖像的頂點是:
(2) 當 \(\displaystyle{ a \lt 0 }\) 時,二次函數圖像的頂點是:
(3) 二次函數的圖像是:
若對稱,圖像的對稱軸是否通過頂點?
(4) 二次函數 \(\displaystyle{y=a{{\left( x-h \right)}^{2}}+k }\) 的頂點坐標是:
(5) 二次函數 \(\displaystyle{y=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right) }\) 的頂點的橫坐標是:
觀察3:二次函數的 \(\displaystyle{ y }\) 軸截距
函數的圖像與 \(\displaystyle{ y }\) 軸的相交點稱為 \(\displaystyle{ y }\) 軸的截距。
(1) 針對二次函數的一般式 \(\displaystyle{y=a{{x}^{2}}+bx+c }\),分別改變 \(\displaystyle{ a }\)、\(\displaystyle{ b }\)、\(\displaystyle{ c}\) 的值,觀察哪個值的改變會影響函數的 \(\displaystyle{ y }\) 軸截距:
該值與 \(\displaystyle{ y }\) 軸截距的關係是:
觀察4:二次函數的 \(\displaystyle{ x }\) 軸截距
函數的圖像與 \(\displaystyle{ x }\) 軸的相交點稱為 \(\displaystyle{ x }\) 軸的截距。
二次函數的 \(\displaystyle{ x }\) 軸截距是其對應的二次方程的根。
(1) 針對二次函數的交點式 \(\displaystyle{ y=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right) }\),分別改變 \(\displaystyle{ a }\)、 \(\displaystyle{ {{x}_{1}} }\)、\(\displaystyle{ {{x}_{2}} }\) 的值,觀察哪個值的改變會影響函數的 \(\displaystyle{ x }\) 軸截距:
思考:如果二次函數對應的二次方程沒有實數解時,即二次方程 \(\displaystyle{ a{{x}^{2}}+bx+c=0\left( a\ne 0 \right) }\) 沒有實數解,那麼二次函數的 \(\displaystyle{ x }\) 軸截距是多少?
此時,二次函數與 \(\displaystyle{ x }\) 軸不相交,所以沒有 \(\displaystyle{ x }\) 軸截距。
觀察5:二次函數的極大值與極小值
在二次函數圖像的最低點處,二次函數的值為極小值;反之,在二次函數圖像的最高點處,二次函數的值為極大值。
(1) 當 \(\displaystyle{ a \gt 0 }\) 時,二次函數:
(2) 當 \(\displaystyle{ a \lt 0 }\) 時,二次函數:
(3) 若二次函數 \(\displaystyle{y=a{{\left( x-h \right)}^{2}}+k }\) 存在極大值或極小值,該值等於:
二次函數的三種不同表示形式展現了函數的不同特徵。
一般式 \(\displaystyle{y=a{{x}^{2}}+bx+c }\) 提供了二次函數的 \(\displaystyle{ y }\) 軸截距 \(\displaystyle{ c }\);
頂點式 \(\displaystyle{y=a{{\left( x-h \right)}^{2}}+k }\) 表示函數的頂點為 \(\displaystyle{\left( h,k \right) }\);
交點式 \(\displaystyle{y=a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right) }\) 提供了二次函數 \(\displaystyle{ x }\) 軸截距為 \(\displaystyle{{{x}_{1}} }\) 和 \(\displaystyle{{{x}_{2}} }\)。
當二次方程 \(\displaystyle{a{{x}^{2}}+bx+c=0\left( a\ne 0 \right) }\) 沒有實數解時,二次函數 \(\displaystyle{y=a{{x}^{2}}+bx+c }\) 與 \(\displaystyle{ x }\) 軸無交點,也就不能寫成交點式。
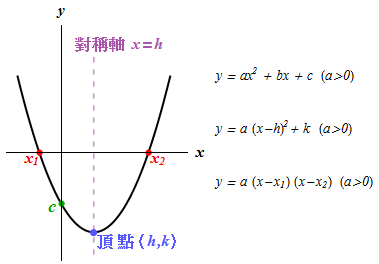
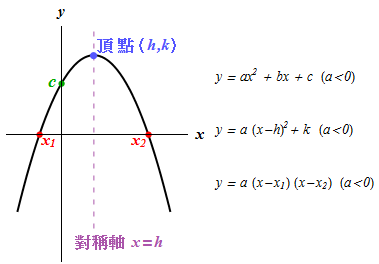
| 二次函數 \(\displaystyle{y=a{{x}^{2}}+bx+c }\) | \(\displaystyle{ a \gt 0 }\) | \(\displaystyle{ a \lt 0 }\) |
|---|---|---|
| 圖像 |
|
|
| 開口方向 | 開口向上 | 開口向下 |
| 對稱軸 (axis of symmetry) | 圖像左右對稱,對稱軸是 \(\displaystyle{ x=h }\) (\(\displaystyle{x=-\frac{b}{2a} }\) 或 \(\displaystyle{x=\frac{{{x}_{1}}+{{x}_{2}}}{2} }\)) | |
| 頂點 | 對稱軸經過頂點,頂點坐標是 \(\displaystyle{\left( h,k \right) }\) | |
| 頂點是最低點 | 頂點是最高點 | |
| \(\displaystyle{ y }\) 軸截距 | \(\displaystyle{ c }\) | |
| \(\displaystyle{ x }\) 軸截距 | \(\displaystyle{{{x}_{1}} }\) 和 \(\displaystyle{ {{x}_{2}} }\) (如果函數圖像與 \(\displaystyle{ x }\) 軸無交點,就沒有 \(\displaystyle{ x }\) 軸截距) | |
| 極值 | 有極小值,是 \(\displaystyle{ k }\) | 有極大值,是 \(\displaystyle{ k }\) |